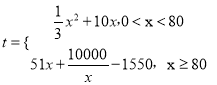题目内容
【题目】学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球.乙箱子里装有1个白球、2个黑球.每次游戏从这两个箱子里随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)求在1次游戏结束后,①摸出3个白球的概率?②获奖的概率?
(2)求在2次游戏中获奖次数X的分布列及数学期望E(X).
【答案】
(1)解:设“摸出3个白球”为事件A,则必须从甲箱子里摸出2个白球,从乙箱子里摸出1个白球与1个黑球.
∴P(A)= ![]() =
= ![]() .
.
②设“获奖”为事件B,B包括两种情况:一种是从甲箱子里摸出1个白球与一个黑球,从乙箱子里摸出1个白球与1个黑球;另一种是从甲箱子里摸出2个白球,从乙箱子里3个球中摸出2个球.
则P(B)= ![]() =
= ![]()
(2)解:由(1)②可知:在1次游戏中,“获奖”的概率P= ![]() ,因此X~B
,因此X~B ![]() .P(X=k)=
.P(X=k)= ![]() ,(k=0,1,2).
,(k=0,1,2).
X | 0 | 1 | 2 |
P |
|
|
|
∴E(X)= ![]() =75
=75
【解析】(1)设“摸出3个白球”为事件A,则必须从甲箱子里摸出2个白球,从乙箱子里摸出1个白球与1个黑球.可得P(A)= ![]() .②设“获奖”为事件B,B包括两种情况:一种是从甲箱子里摸出1个白球与一个黑球,从乙箱子里摸出1个白球与1个黑球;另一种是从甲箱子里摸出2个白球,从乙箱子里3个球中摸出2个球.可得P(B).(2)由(1)②可知:在1次游戏中,“获奖”的概率P=
.②设“获奖”为事件B,B包括两种情况:一种是从甲箱子里摸出1个白球与一个黑球,从乙箱子里摸出1个白球与1个黑球;另一种是从甲箱子里摸出2个白球,从乙箱子里3个球中摸出2个球.可得P(B).(2)由(1)②可知:在1次游戏中,“获奖”的概率P= ![]() ,因此X~B
,因此X~B ![]() .利用P(X=k)=
.利用P(X=k)= ![]() ,(k=0,1,2),即可得出分布列与数学期望.
,(k=0,1,2),即可得出分布列与数学期望.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.

【题目】探究函数![]() 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题.
函数![]() 在区间(0,2)上递减;
在区间(0,2)上递减;
函数![]() 在区间 上递增.
在区间 上递增.
当![]() 时,
时, ![]() .
.
证明:函数![]() 在区间(0,2)递减.
在区间(0,2)递减.
思考:函数![]() 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
【题目】某地区2009年至2015年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 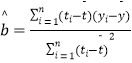 .
. ![]() .
.
参考数据:(﹣3)×(﹣1.4)+(﹣2)×(﹣1)+(﹣1)×(﹣0.7)+1×0.5+2×0.9+3×1.6=14.