题目内容
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1﹣x).
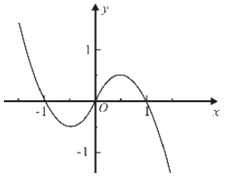
(1)在如图所给直角坐标系中画出函数f(x)的草图,并直接写出函数f(x)的零点;
(2)求出函数f(x)的解析式.
【答案】解:(1)当x≥0时,由f(x)=2x(1﹣x)=0得x=0或x=1,
∵f(x)是定义在R上的奇函数,
∴当x<0时,函数的零点为﹣1,
即函数f(x)的零点为0,﹣1,1.
(2)若x<0,则﹣x>0,
∵x≥0时,f(x)=2x(1﹣x).
∴当﹣x>0时,f(﹣x)=﹣2x(1+x).
∵f(x)是定义在R上的奇函数,
∴f(﹣x)=﹣2x(1+x)=﹣f(x),
即f(x)=2x(1+x),x<0.
即f(x)=![]() .
.
【解析】(1)根据函数奇偶性的性质以及函数零点的定义进行求解即可.
(2)根据函数奇偶性的性质进行转化求解即可.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

练习册系列答案
相关题目