Question

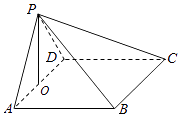
【题目】如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（12分）

（1）证明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC，∠APD=90°，且四棱锥P﹣ABCD的体积为 ，求该四棱锥的侧面积．

Answer 1

【答案】
（1）

证明：∵在四棱锥P﹣ABCD中，∠BAP=∠CDP=90°，

∴AB⊥PA，CD⊥PD，

又AB∥CD，∴AB⊥PD，

∵PA∩PD=P，∴AB⊥平面PAD，

∵AB平面PAB，∴平面PAB⊥平面PAD．

（2）

解：设PA=PD=AB=DC=a，取AD中点O，连结PO，

∵PA=PD=AB=DC，∠APD=90°，平面PAB⊥平面PAD，

∴PO⊥底面ABCD，且AD= = ，PO= ，

∵四棱锥P﹣ABCD的体积为 ，

∴VP﹣ABCD=

= = = =8，

解得a=2，∴PA=PD=AB=DC=2，AD=BC=2 ，PO= ，

∴PB=PC= =2 ，

∴该四棱锥的侧面积：

S侧=S△PAD+S△PAB+S△PDC+S△PBC

= + + +

=

=6+2 ．

【解析】（1.）推导出AB⊥PA，CD⊥PD，从而AB⊥PD，进而AB⊥平面PAD，由此能证明平面PAB⊥平面PAD．
（2.）设PA=PD=AB=DC=a，取AD中点O，连结PO，则PO⊥底面ABCD，且AD= ，PO= ，由四棱锥P﹣ABCD的体积为 ，求出a=2，由此能求出该四棱锥的侧面积．
【考点精析】关于本题考查的平面与平面垂直的判定，需要了解一个平面过另一个平面的垂线，则这两个平面垂直才能得出正确答案．