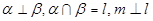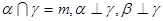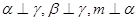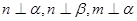题目内容
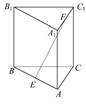
如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB^平面PAD,△PAD是正三角形,
DC//AB,DA=DC=2AB.
(1)若点E为棱PA上一点,且OE∥平面PBC,求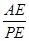 的值;
的值;
(2)求证:平面PBC^平面PDC.
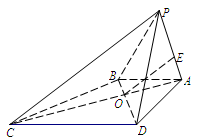
DC//AB,DA=DC=2AB.
(1)若点E为棱PA上一点,且OE∥平面PBC,求
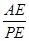 的值;
的值;(2)求证:平面PBC^平面PDC.

(1)详见解析;(2)详见解析.
试题分析: (1)由题中所给条件,不难联想到要运用线面平行的性质定理将线面平行转化为线线平行,即由
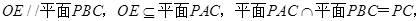 所以
所以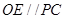 ,再结合平面几何的知识易得:
,再结合平面几何的知识易得: 结合比例线段关系即可求得
结合比例线段关系即可求得 ;(2)中要证明面面垂直,根据面面垂直的判定定理可转化为证明线面垂直,由题中的数量关系不难发现取
;(2)中要证明面面垂直,根据面面垂直的判定定理可转化为证明线面垂直,由题中的数量关系不难发现取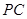 的中点
的中点 ,连结
,连结 ,运用解三角形的知识算出
,运用解三角形的知识算出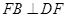 ,问题即可得证.
,问题即可得证. 试题解析: (1)因为
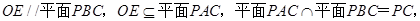 所以
所以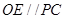 ,
,所以
 . 3分
. 3分因为
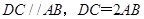 ,所以
,所以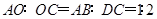 .
.所以
 . 6分
. 6分(2)取
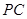 的中点
的中点 ,连结
,连结 .
.因为
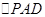 是正三角形,
是正三角形,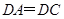 ,所以
,所以 .
.因为
 为
为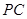 的中点,所以
的中点,所以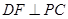 . 8分
. 8分因为
 ,所以
,所以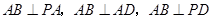 .
.因为
 ,所以
,所以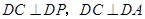 .
.设
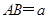 ,在等腰直角三角形
,在等腰直角三角形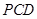 中,
中, .
.在
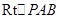 中,
中,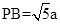 .
.在直角梯形
 中,
中,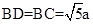 .
.因为
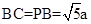 ,点F为PC的中点,所以
,点F为PC的中点,所以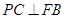 .
.在
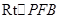 中,
中,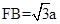 .
. 在
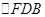 中,由
中,由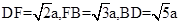 ,可知
,可知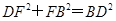 ,所以
,所以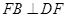 .
.12分
由
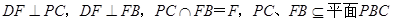 ,所以
,所以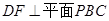 .
.又
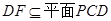 ,所以平面
,所以平面 14分
14分
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
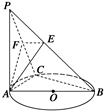
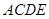 所在的平面与平面
所在的平面与平面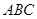 垂直,
垂直,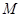 是
是 和
和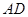 的交点,
的交点,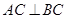 ,且
,且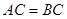 .
.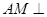 平面
平面 ;
; 的大小.
的大小.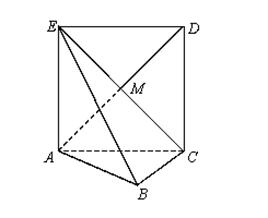

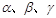 为平面,
为平面,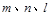 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为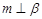 的一个充分条件的是( )
的一个充分条件的是( )