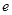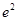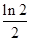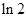题目内容
设点P在曲线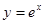 上,点Q在曲线
上,点Q在曲线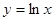 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )
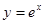 上,点Q在曲线
上,点Q在曲线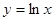 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )A.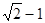 | B.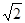 | C. | D.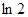 |
B.
试题分析:因为函数
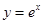 与
与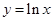 互为反函数所以它们的图象关于直线
互为反函数所以它们的图象关于直线 对称,要使
对称,要使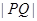 最小,则必有过
最小,则必有过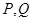 两点的切线斜率和
两点的切线斜率和 的斜率相等,对于曲线
的斜率相等,对于曲线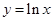 ,令
,令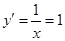 ,得
,得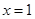 ,故
,故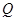 点坐标为
点坐标为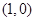 ;同理,对于曲线
;同理,对于曲线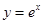 ,令
,令 ,得
,得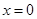 ,所以
,所以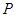 点坐标为
点坐标为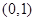 ,综上,
,综上,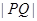 最小值为
最小值为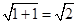 ,选B.
,选B.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
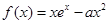 .
.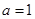 时,求
时,求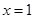 处的切线方程;
处的切线方程;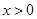 时,
时,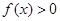 ,求
,求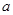 的取值范围.
的取值范围.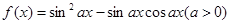 的图象与直线
的图象与直线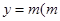 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为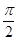
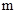 的值;
的值; 是
是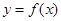 图象的对称中心,且
图象的对称中心,且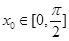 ,求点A的坐标
,求点A的坐标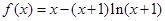 (
(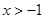 ).
).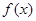 的单调区间;
的单调区间;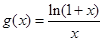 (
(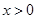 )的单调性证明:当
)的单调性证明:当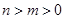 时,
时,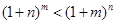 ;
;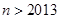 ,且
,且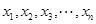 均为正实数,
均为正实数, 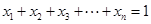 时,
时,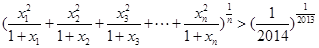 .
.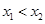 ,求证:
,求证: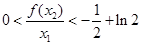 .
.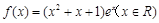 的单调减区间为
的单调减区间为 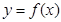 定义域为
定义域为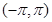 ,且函数
,且函数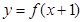 的图象关于直线
的图象关于直线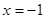 对称,当
对称,当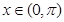 时,
时,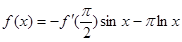 ,(其中
,(其中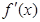 是
是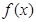 的导函数),若
的导函数),若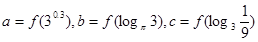 ,则
,则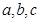 的大小关系是( )
的大小关系是( )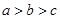
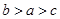
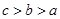
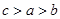
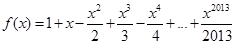 ,
,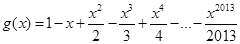 ,设函数
,设函数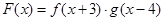 ,且函数
,且函数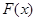 的零点均在区间
的零点均在区间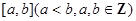 内,则
内,则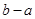 的最小值为( )
的最小值为( )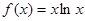 ,若
,若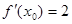 ,则
,则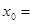 ( )
( )