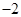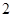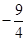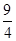题目内容
已知函数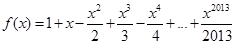 ,
,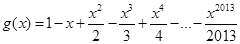 ,设函数
,设函数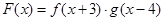 ,且函数
,且函数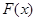 的零点均在区间
的零点均在区间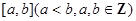 内,则
内,则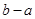 的最小值为( )
的最小值为( )
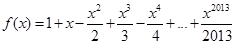 ,
,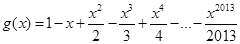 ,设函数
,设函数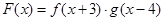 ,且函数
,且函数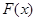 的零点均在区间
的零点均在区间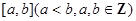 内,则
内,则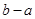 的最小值为( )
的最小值为( )| A.11 | B.10 | C.9 | D.8 |
B
试题分析:
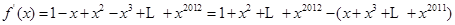
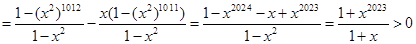 ,所以
,所以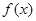 在
在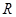 上单调递增,
上单调递增,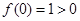 ,
,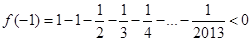 ,所以
,所以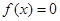 的零点在
的零点在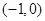 上,而
上,而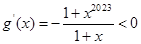 ,所以
,所以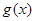 在
在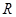 上单调递减,
上单调递减,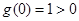 ,
,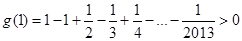 ,
, 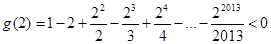 ,所以
,所以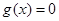 的零点在
的零点在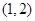 上,函数
上,函数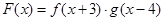 ,且函数
,且函数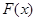 的零点均在区间
的零点均在区间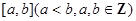 内,
内,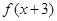 的零点在
的零点在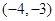 上,
上,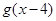 的零点在
的零点在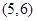 上,
上,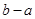 的最小值为
的最小值为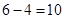 .
.
练习册系列答案
相关题目
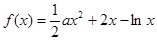
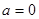 时,求
时,求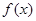 的极值;
的极值; 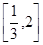 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.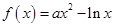 (
(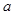 为常数).
为常数).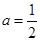 时,求
时,求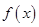 的单调递减区间;
的单调递减区间;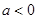 ,且对任意的
,且对任意的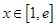 ,
,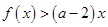 恒成立,求实数
恒成立,求实数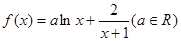 .
.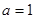 时,求
时,求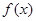 在
在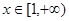 最小值;
最小值;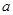 的取值范围;
的取值范围;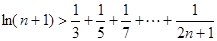 (
(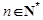 ).
).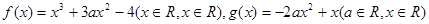 (Ⅰ)若函数
(Ⅰ)若函数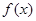 在
在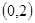 上单调递减,在区间
上单调递减,在区间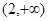 单调递增,求
单调递增,求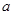 的值;
的值;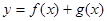 在
在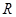 上有两个不同的极值点,求
上有两个不同的极值点,求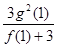 的取值范围;
的取值范围;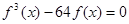 有且只有三个不同的实根,求
有且只有三个不同的实根,求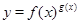 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: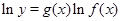 ,再两边同时求导得
,再两边同时求导得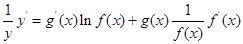 ,于是得到:
,于是得到: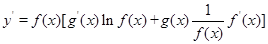 ,运用此方法求得函数
,运用此方法求得函数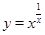 的一个单调递增区间是( )
的一个单调递增区间是( )


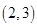
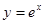 上,点Q在曲线
上,点Q在曲线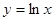 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )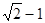
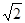

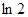
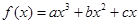 在点
在点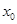 处取得极小值-4,使其导数
处取得极小值-4,使其导数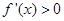 的
的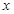 的取值范围为
的取值范围为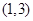 ,求:
,求: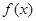 的解析式;
的解析式;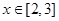 ,求
,求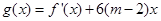 的最大值;
的最大值;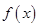 的导数为
的导数为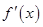 ,且满足关系式
,且满足关系式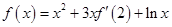 则
则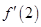 的值等于( )
的值等于( )