题目内容
设函数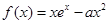 .
.
(1)若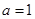 时,求
时,求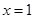 处的切线方程;
处的切线方程;
(2)当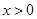 时,
时,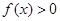 ,求
,求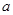 的取值范围.
的取值范围.
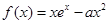 .
.(1)若
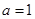 时,求
时,求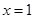 处的切线方程;
处的切线方程;(2)当
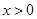 时,
时,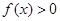 ,求
,求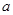 的取值范围.
的取值范围.(1)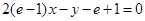 ;(2)
;(2)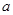 的取值范围是
的取值范围是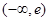 .
.
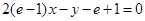 ;(2)
;(2)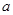 的取值范围是
的取值范围是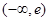 .
.试题分析:本题考查函数与导数及运用导数求单调区间、最值等数学知识和方法,突出考查综合运用数学知识和方法分析问题解决问题的能力.第一问,将
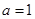 代入得到
代入得到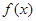 解析式,对
解析式,对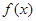 求导,将
求导,将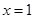 代入得到切线的斜率,再将
代入得到切线的斜率,再将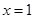 代入
代入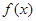 中得到切点的纵坐标,最后利用点斜式方程直接写出切线方程;第二问,将恒成立问题转化成函数
中得到切点的纵坐标,最后利用点斜式方程直接写出切线方程;第二问,将恒成立问题转化成函数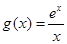 的最小值问题,对
的最小值问题,对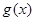 求导,判断
求导,判断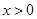 范围内的函数的单调性,判断出当
范围内的函数的单调性,判断出当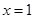 时,
时,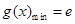 ,所以
,所以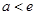 .
.试题解析:(1)当
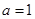 ,
,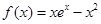
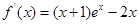 ,
,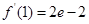 ,
, ,
,故所求切线方程为:
 ,
,化简得:
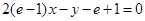 .(5分)
.(5分)(2)
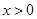 ,
, ,
,化简得:
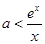 ,
,设
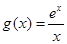 ,
,求导得:
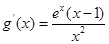 .
.当
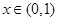 时,
时,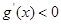 ;当
;当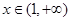 时,
时,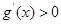 .
.故
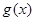 在
在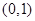 单调减少,在
单调减少,在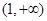 单调增加.
单调增加.故
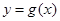 在
在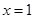 时取极小值.
时取极小值.则
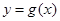 在
在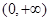 时,
时,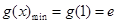 .
.综上所述:
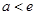 ,即
,即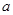 的取值范围是
的取值范围是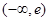 .(13分)
.(13分)
练习册系列答案
相关题目
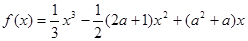 .
.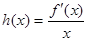 为奇函数,求a的值;
为奇函数,求a的值;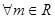 ,直线
,直线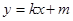 都不是曲线
都不是曲线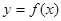 的切线,求k的取值范围;
的切线,求k的取值范围;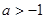 ,求
,求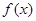 在区间
在区间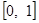 上的最大值.
上的最大值.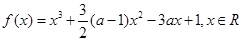 .
. 的单调区间;
的单调区间;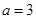 时,若函数
时,若函数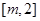 上的最大值为28,求
上的最大值为28,求 的取值范围.
的取值范围.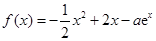 .
.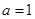 ,求
,求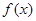 在
在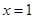 处的切线方程;
处的切线方程;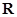 上是增函数,求实数
上是增函数,求实数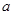 的取值范围.
的取值范围.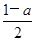
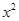 +ax-lnx(a∈R).
+ax-lnx(a∈R).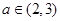 及任意
及任意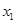 ,
,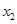 ∈[1,2],恒有
∈[1,2],恒有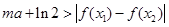 成立,求实数m的取值范围.
成立,求实数m的取值范围.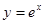 上,点Q在曲线
上,点Q在曲线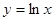 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )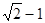
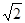

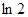
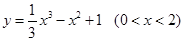 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为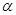 ,则
,则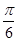
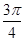
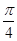
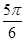
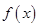 的导数为
的导数为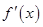 ,且满足关系式
,且满足关系式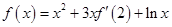 则
则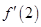 的值等于( )
的值等于( )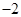
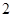
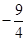
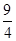
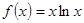 ,若
,若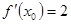 ,则x0等于 ( )
,则x0等于 ( )


