题目内容
已知函数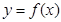 定义域为
定义域为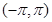 ,且函数
,且函数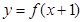 的图象关于直线
的图象关于直线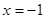 对称,当
对称,当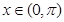 时,
时,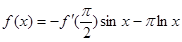 ,(其中
,(其中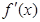 是
是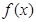 的导函数),若
的导函数),若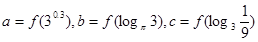 ,则
,则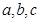 的大小关系是( )
的大小关系是( )
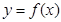 定义域为
定义域为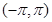 ,且函数
,且函数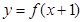 的图象关于直线
的图象关于直线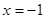 对称,当
对称,当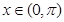 时,
时,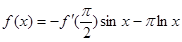 ,(其中
,(其中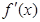 是
是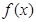 的导函数),若
的导函数),若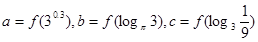 ,则
,则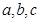 的大小关系是( )
的大小关系是( )A.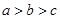 | B.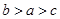 | C.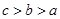 | D.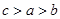 |
B
试题分析:因为
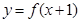 是将
是将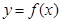 的图象向左平移
的图象向左平移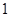 个单位得到,而其图象关于直线
个单位得到,而其图象关于直线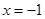 对称,故
对称,故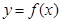 的图象关于
的图象关于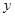 轴对称,可见
轴对称,可见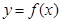 为偶函数,又
为偶函数,又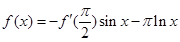 ,所以
,所以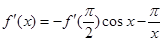 ,令
,令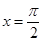 得
得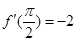 ,所以
,所以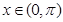 时,
时,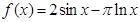 ,且为偶函数,而
,且为偶函数,而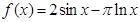 在
在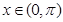 减,因为
减,因为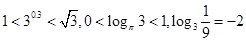 ,而
,而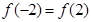 ,所以
,所以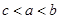 ,选B.
,选B.
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
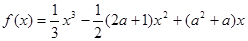 .
.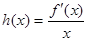 为奇函数,求a的值;
为奇函数,求a的值;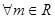 ,直线
,直线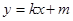 都不是曲线
都不是曲线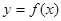 的切线,求k的取值范围;
的切线,求k的取值范围;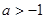 ,求
,求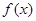 在区间
在区间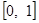 上的最大值.
上的最大值.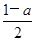
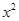 +ax-lnx(a∈R).
+ax-lnx(a∈R).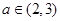 及任意
及任意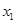 ,
,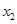 ∈[1,2],恒有
∈[1,2],恒有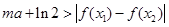 成立,求实数m的取值范围.
成立,求实数m的取值范围.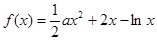
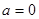 时,求
时,求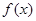 的极值;
的极值; 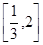 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.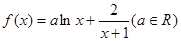 .
.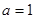 时,求
时,求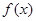 在
在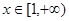 最小值;
最小值;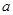 的取值范围;
的取值范围;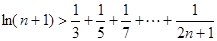 (
(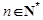 ).
).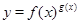 的函数的导数,我们常采用以下做法:先两边同取自然对数得:
的函数的导数,我们常采用以下做法:先两边同取自然对数得: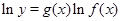 ,再两边同时求导得
,再两边同时求导得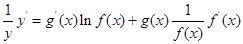 ,于是得到:
,于是得到: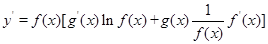 ,运用此方法求得函数
,运用此方法求得函数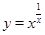 的一个单调递增区间是( )
的一个单调递增区间是( )


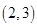
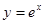 上,点Q在曲线
上,点Q在曲线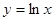 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )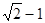
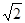

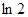
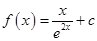 (
(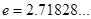 是自然对数的底数,
是自然对数的底数,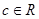 ).
).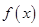 的单调区间、最大值;
的单调区间、最大值;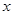 的方程
的方程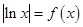 根的个数。
根的个数。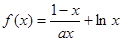 的导函数是
的导函数是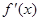 ,则
,则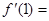 .
.