题目内容
【题目】（本小题满分12分）设等差数列｛an｝的前n项和为Sn，且S4=4S2，a2n=2an+1
（1） 求数列｛an｝的通项公式；
（2） 设数列｛bn｝的前n项和Tn，且Tn+
= λ（λ为常数），令cn=b2n，（n∈N）.求数列｛cn｝的前n项和Rn.
【答案】（1）
（2）
【解析】试题分析：根据等差数列的通项公式和前
项和公式，依据题意列方程组，解方程组解出
和
，写出通项公式；根据
，把
替换为
，两式相减，得出
，再用错位相减法求出
.
试题解析：（1）由S4=4S2，a2n=2an+1，｛an｝为等差数列，可得
，
即： 
……(1) ，
又
，即
……(2)
联立（1）（2）得： 
，所以
（2）由Tn+
= λ，当
时， 可得
，当
时，Tn-1+
= λ两式相减
，所以当
时， 
，利用错位相减法可得
当
时， 
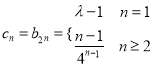，可得
练习册系列答案
相关题目
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
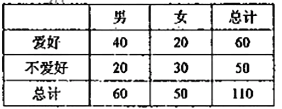
由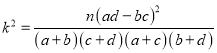
算得， 
.
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
则参照附表，得到的正确结论应是( )
A. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”
