题目内容
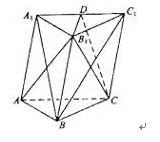
如图,四面体ABCD中,O、E分别是BD、BC的中点,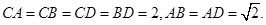
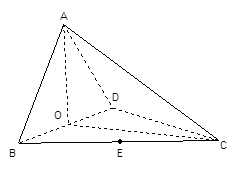
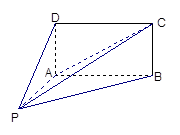
(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦值;
(III)求点E到平面ACD的距离。
(I)连结OC,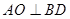
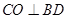
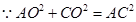


 平面
平面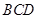
(II)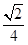 (III)
(III)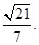
解析试题分析:(I)证明:连结OC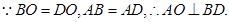
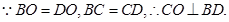
在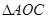 中,由已知可得
中,由已知可得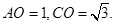
而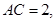
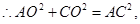
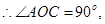 即
即
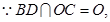
 平面
平面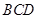
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知
 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在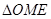 中,
中,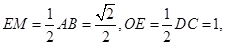
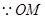 是直角
是直角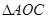 斜边AC上的中线,
斜边AC上的中线,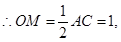
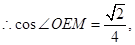
(III)解:设点E到平面ACD的距离为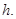
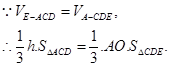 在
在 中,
中,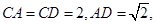
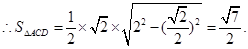 而
而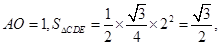
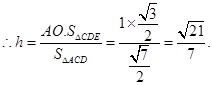
 点E到平面ACD的距离为
点E到平面ACD的距离为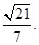
考点:线面垂直的判定异面直线所成角及点面距
点评:本题还可用空间向量来证明计算

练习册系列答案
相关题目
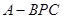 中,
中, ,
,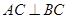 ,
, 为
为 中点,
中点, 为
为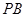 中点,且
中点,且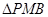 为正三角形.
为正三角形.
 平面
平面 .
. ⊥平面
⊥平面 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得. 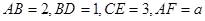 ,
, 为
为 的中点.
的中点.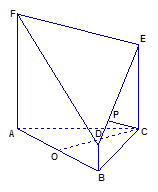
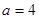 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱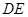 上存在点
上存在点 ,使
,使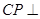 平面
平面 中,
中,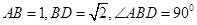 ,将它们沿对角线
,将它们沿对角线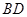 折起,折后的点
折起,折后的点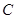 变为
变为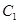 ,且
,且 .
.
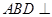 平面
平面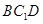 ;
;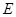 为线段
为线段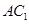 上的一个动点,当线段
上的一个动点,当线段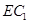 的长为多少时,
的长为多少时, 与平面
与平面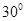 ?
?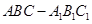 的侧面
的侧面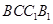 是菱形,
是菱形,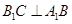
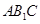
 平面
平面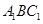 ;
; 是
是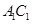 上的点,且
上的点,且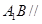 平面
平面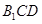 ,求
,求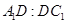 的值.
的值. 中,
中, 为正方形,
为正方形,
 分别是线段
分别是线段 的中点. 求证:
的中点. 求证: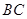 //平面
//平面 ;
;  .
.
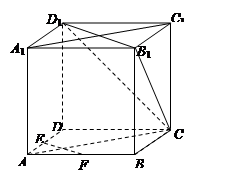
 中,底面ABCD是边长为1的正方形,
中,底面ABCD是边长为1的正方形, 平面ABCD,PA=AB,M,N分别为PB,AC的中点,
平面ABCD,PA=AB,M,N分别为PB,AC的中点, 
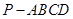 的底面
的底面 为矩形,且
为矩形,且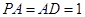 ,
,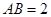 ,
,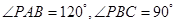 ,(Ⅰ)平面
,(Ⅰ)平面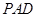 与平面
与平面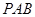 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线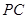 与平面
与平面