题目内容
如图,在三棱锥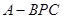 中,
中, ,
,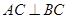 ,
, 为
为 中点,
中点,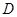 为
为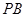 中点,且
中点,且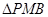 为正三角形.
为正三角形.
(1)求证: 平面
平面 .
.
(2)求证:平面 ⊥平面
⊥平面 .
.
(1)只需证MD//AP;(2)只需证BC⊥平面APC。
解析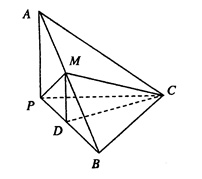
试题分析:(1)∵M为AB中点,D为PB中点,
∴MD//AP,
又MD 平面ABC, AP
平面ABC, AP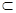 平面ABC
平面ABC
∴MD//平面APC
(2)∵△PMB为正三角形,且D为PB中点,
∴MD⊥PB.
又由(Ⅰ)知MD//AP,
∴AP⊥PB.
又已知AP⊥PC,PB∩PC=P
∴AP⊥平面PBC,而BC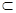 平面PBC,
平面PBC,
∴AP⊥BC,
又AC⊥BC,而AP∩AC="A,"
∴BC⊥平面APC,
又BC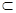 平面ABC
平面ABC
∴平面ABC⊥平面PAC
考点:线面平行的判定定理;面面垂直的判定定理;线面垂直的判定定理。
点评:证明线面平行的常用方法:①定义:若一条直线和一个平面没有公共点,则它们平行;
②线线平行Þ线面平行
若平面外的一条直线平行于平面内的一条直线,则它与这个平面平行。 即
即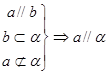
③面面平行Þ线面平行
若两平面平行,则其中一个平面内的任一条直线平行于另一个平面。 即
即

练习册系列答案
相关题目

 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,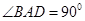 ,
,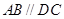 ,
, ,且PA=AD=DC=
,且PA=AD=DC=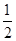 AB=1.
AB=1.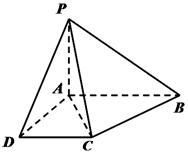
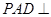 平面
平面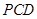
 与
与 所成角的余弦值
所成角的余弦值 中,
中,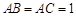 ,
,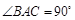 ,且异面直线
,且异面直线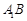 与
与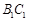 所成的角等于
所成的角等于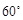 .
.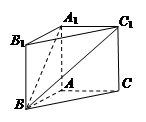
 所成的角的大小.
所成的角的大小.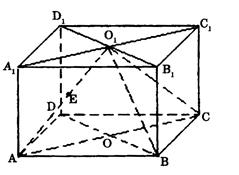
 平面O1BD
平面O1BD 中,
中, 于
于 ,
, ,将
,将 沿
沿 折起,使
折起,使 .
.
 平面
平面 ;
;  和平面
和平面 夹角的余弦值.
夹角的余弦值. 中,
中,
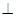 平面
平面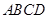 ,底面
,底面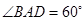 .
.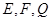 分别是
分别是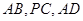 的中点.
的中点.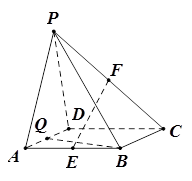
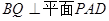 ;
;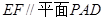 .
. 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.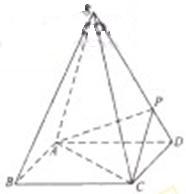
 平面BCD;
平面BCD;