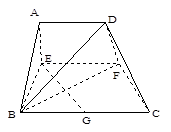题目内容
(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.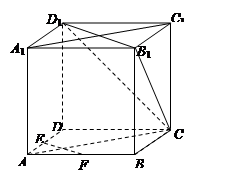
(1)求证:EF ∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
(1)见解析;(2)见解析。
解析试题分析:(1)连结BD
在正方体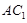 中,对角线
中,对角线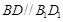 .
.
又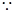 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,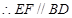 .
. 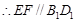 .
.
又B1D1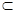 平面
平面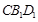 ,
,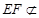 平面
平面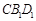 ,
, EF∥平面CB1D1.
EF∥平面CB1D1.
(2) 在正方体
在正方体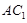 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1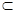 平面A1B1C1D1,
平面A1B1C1D1, AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,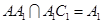
 B1D1⊥平面CAA1C1. 又
B1D1⊥平面CAA1C1. 又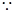 B1D1
B1D1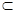 平面CB1D1,
平面CB1D1,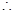 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.
考点:线面垂直的判定定理;面面垂直的判定定理。
点评:本题第一问的关键是证得B1D1∥EF;第二问的关键是熟练掌握空间中线线垂直、线面垂直、面面垂直之间的相互转化。

练习册系列答案
相关题目
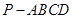 中,
中,
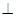 平面
平面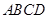 ,底面
,底面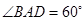 .
.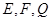 分别是
分别是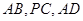 的中点.
的中点.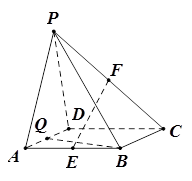
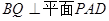 ;
;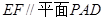 .
.
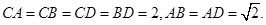
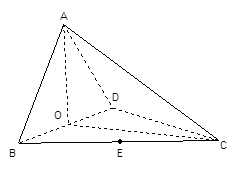
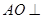 平面BCD;
平面BCD;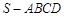 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,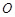 是
是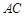 与
与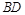 的交点,
的交点,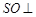 平面
平面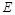 是侧棱
是侧棱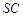 的中点,异面直线
的中点,异面直线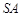 和
和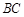 所成角的大小是60
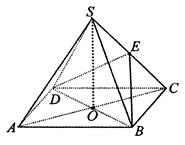
所成角的大小是60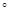 .
.
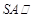 平面
平面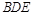 ;
;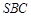 所成角的正弦值.
所成角的正弦值.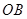 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为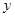 ,
,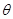 (rad),将y表示成
(rad),将y表示成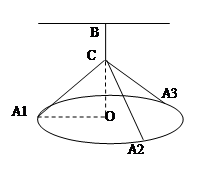
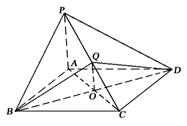
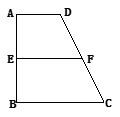
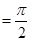 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE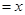 ,G是BC的中点.沿EF将梯形ABCD翻折,
,G是BC的中点.沿EF将梯形ABCD翻折,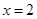 时,求证:BD⊥EG ;
时,求证:BD⊥EG ;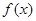 ,求
,求