题目内容
[2014·济南模拟]已知曲线y1=2- 与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
| A.-2 | B.2 | C. | D.1 |
D
解析

练习册系列答案
相关题目
定义在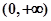 上的单调递减函数
上的单调递减函数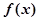 ,若
,若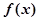 的导函数存在且满足
的导函数存在且满足 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. | B.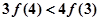 |
C.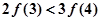 | D.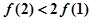 |
设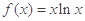 ,若
,若 ,则
,则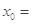 ( )
( )
A.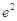 | B.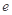 | C.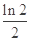 | D.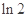 |
设函数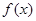 在R上存在导数
在R上存在导数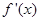 ,对任意的
,对任意的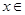 R,有
R,有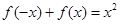 ,且
,且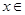 (0,+
(0,+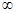 )时,
)时,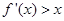 .若
.若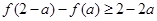 ,则实数a的取值范围为( )
,则实数a的取值范围为( )
| A.[1,+∞) | B.(-∞,1] | C.(-∞,2] | D.[2,+∞) |
函数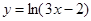 上过点(1,0)的切线方程( )
上过点(1,0)的切线方程( )
A.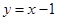 | B. | C.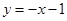 | D. |
设曲线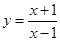 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线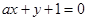 垂直,则
垂直,则 的值是
的值是
| A.2 | B.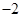 | C.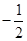 | D.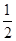 |
函数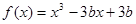 在
在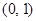 内有极小值,则
内有极小值,则
A.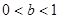 | B.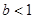 | C.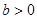 | D.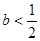 |
已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
| A.?x0∈R,f(x0)=0 |
| B.函数y=f(x)的图象是中心对称图形 |
| C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 |
| D.若x0是f(x)的极值点,则f′(x0)=0 |
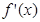 是函数
是函数 的导函数,将
的导函数,将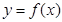 和
和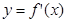 的图像画在同一个直角坐标系中,不可能正确的是( )
的图像画在同一个直角坐标系中,不可能正确的是( )