题目内容
设曲线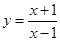 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线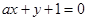 垂直,则
垂直,则 的值是
的值是
| A.2 | B.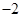 | C.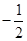 | D.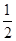 |
B
解析试题分析:函数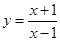 =1+
=1+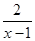 的导数为
的导数为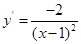 ,
,
∴曲线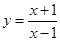 在点(3,2)处的切线斜率为
在点(3,2)处的切线斜率为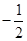 ,
,
由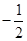 ×(-a)="-1" 得,a=-2,故答案为:B.
×(-a)="-1" 得,a=-2,故答案为:B.
考点: 函数在某点的导数值与曲线在此点的切线的斜率的关系;两直线垂直的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知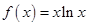 ,若
,若 则
则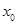 等于( )
等于( )
A.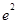 | B.e | C.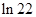 | D.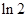 |
已知函数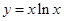 ,则这个函数在点
,则这个函数在点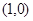 处的切线方程是( )
处的切线方程是( )
A.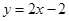 | B.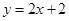 | C.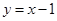 | D.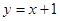 |
若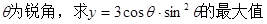 是( )
是( )
| A.3 | B.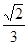 | C.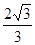 | D.1 |
直线y=kx+1与曲线y=x3+ax+b相切于点A(1,3),则2a+b的值为( )
| A.2 | B.-1 | C.1 | D.-2 |
函数 的单调递减区间是( )
的单调递减区间是( )
A.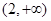 | B.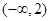 | C.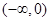 | D. |
已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是( )
| A.-37 | B.-29 | C.-5 | D.以上都不对 |
[2014·济南模拟]已知曲线y1=2- 与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
| A.-2 | B.2 | C. | D.1 |
若f(x)=ax4+bx2+c满足f′(1)=2,则f′(﹣1)=( )
| A.﹣4 | B.﹣2 | C.2 | D.4 |