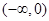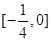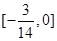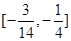题目内容
函数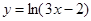 上过点(1,0)的切线方程( )
上过点(1,0)的切线方程( )
A.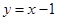 | B. | C.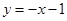 | D. |
B
解析试题分析:因为 ,在点(1,0)处的斜率为
,在点(1,0)处的斜率为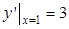 ,所以在点(1,0)处的切线方程为y-0=3(x-1),即y=3x-3.
,所以在点(1,0)处的切线方程为y-0=3(x-1),即y=3x-3.
考点:导数的几何意义.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
若函数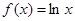 ,则
,则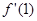 等于( )
等于( )
A. | B. | C.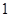 | D. |
若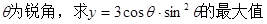 是( )
是( )
| A.3 | B.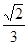 | C.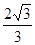 | D.1 |
定义在R上的函数f(x)的导函数为f′(x),已知f(x+1)是偶函数,(x-1)f′(x)<0.若x1<x2,且x1+x2>2,则f(x1)与f(x2)的大小关系是( )
| A.f(x1)<f(x2) | B.f(x1)=f(x2) |
| C.f(x1)>f(x2) | D.不确定 |
[2014·济南模拟]已知曲线y1=2- 与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
与y2=x3-x2+2x在x=x0处切线的斜率的乘积为3,则x0的值为( )
| A.-2 | B.2 | C. | D.1 |
已知a≤ +ln x对任意x∈[
+ln x对任意x∈[ ,2]恒成立,则a的最大值为( )
,2]恒成立,则a的最大值为( )
| A.0 | B.1 | C.2 | D.3 |
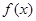 )是定义在(一
)是定义在(一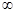 ,0)上的可导函数,其导函数为
,0)上的可导函数,其导函数为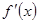 ,且有
,且有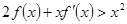 ,则不等式
,则不等式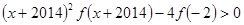 的解集为-------------
的解集为-------------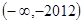 B.
B.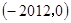 C.
C.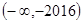 D.
D. 
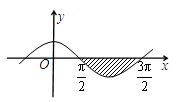
 的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )
的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )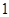



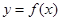 定义域内的一个子区间,若存在
定义域内的一个子区间,若存在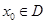 ,使
,使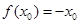 ,则称
,则称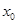 是
是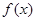 的一个“次不动点”,也称
的一个“次不动点”,也称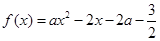 在区间
在区间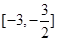 上存在次不动点,则实数a的取值范围是( )
上存在次不动点,则实数a的取值范围是( )