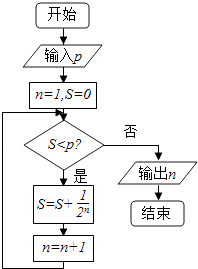
题目内容
【题目】已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【答案】(1)![]() =1(2)直线l不存在
=1(2)直线l不存在
【解析】(1)依题意,可设椭圆C的方程为![]() =1(a>b>0),且可知左焦点为F′(-2,0).
=1(a>b>0),且可知左焦点为F′(-2,0).
从而有![]() 解得
解得![]()
又a2=b2+c2,所以b2=12,故椭圆C的方程为![]() =1.
=1.
(2)假设存在符合题意的直线l,由题知直线l的斜率与直线OA的斜率相等,故可设直线l的方程为y=![]() x+t.由
x+t.由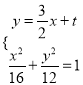 得3x2+3tx+t2-12=0.
得3x2+3tx+t2-12=0.
因为直线l与椭圆C有公共点,所以Δ=(3t)2-4×3(t2-12)≥0,解得-4![]() ≤t≤4
≤t≤4![]() .
.
另一方面,由直线OA与l的距离d=4,可得![]() =4,从而t=±2
=4,从而t=±2![]() .由于±2
.由于±2![]() [-4
[-4![]() ,4
,4![]() ],所以符合题意的直线l不存在
],所以符合题意的直线l不存在

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段,下表是初赛成绩(得分均为整数,满分为100分)的频率分布表.
分组(分数段) | 频数(人数) | 频率 |
|
| 0.16 |
| 17 |
|
| 19 | 0.38 |
|
|
|
合计 | 50 | 1 |
(Ⅰ)求频率分布表中![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答3道判断题,答对3道题获得一等奖,答对2道题获得二等奖,答对1道题获得三等奖,否则不得奖.若某同学进入决赛,且其每次答题回答正确与否均是等可能的,试列出他回答问题的所有可能情况,并求出他至少获得二等奖的概率.