题目内容
18.已知集合A=$\left\{{({x,y})|\left\{{\begin{array}{l}{x+y-1≤0}\\{x-y-3≤0}\\{x≥1}\end{array}}\right.}\right\},B\left\{{({x,y})|{{({x-2})}^2}+{{({y-2})}^2}≤{R^2},R>0}\right\}$.且A∩B≠ϕ,R的最小值为( )| A. | $\frac{{2\sqrt{3}}}{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
分析 分别画出集合A,B,如图所示,得到圆心A得坐标为(2,2),点B的坐标为(1,0),因为A∩B≠ϕ,得到R≥AB,问题得以解决.
解答 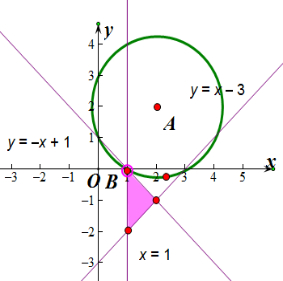 解:分别画出集合A,B,如图所示,
解:分别画出集合A,B,如图所示,
得到圆心A得坐标为(2,2),点B的坐标为(1,0),
∴AB=$\sqrt{(2-1)^{2}+{2}^{2}}$=$\sqrt{5}$
∵A∩B≠ϕ,
∴R≥AB=$\sqrt{5}$,
∴R的最小值为$\sqrt{5}$,
故选:B
点评 本题考查了交集及其运算,熟练掌握交集的定义是解本题的关键,属于基础题.

练习册系列答案
相关题目
6.若x,y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{y≤2}\\{x≤2y}\end{array}\right.$则目标函数z=x2+y2的最小值为( )
| A. | $\frac{20}{9}$ | B. | 2 | C. | 3 | D. | 4 |
10.已知数列{an}共有5项,满足a1>a2>a3>a4>a5≥0,且对任意i、j(1≤i≤j≤5),有ai-aj仍是该数列的某一项,现给出下列4个命题:
(1)a5=0;
(2)4a4=a1;
(3)数列{an}是等差数列;
(4)集合A={x|x=ai+aj,1≤i≤j≤5}中共有9个元素.
则其中真命题的序号是( )
(1)a5=0;
(2)4a4=a1;
(3)数列{an}是等差数列;
(4)集合A={x|x=ai+aj,1≤i≤j≤5}中共有9个元素.
则其中真命题的序号是( )
| A. | (1)、(2)、(3)、(4) | B. | (1)、(4) | C. | (2)、(3) | D. | (1)、(3)、(4) |
8.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y-8≤0}\end{array}\right.$所表示的平面区域是α,不等式组$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤10\end{array}\right.$所表示的平面区域为α,在区域α内随机取一点P,则点P落在区域β内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{4}$ |