题目内容
已知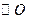 、
、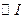 分别是
分别是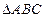 的外接圆和内切圆;证明:过
的外接圆和内切圆;证明:过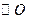 上的任意一点
上的任意一点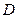 ,都可作一个三角形
,都可作一个三角形 ,使得
,使得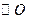 、
、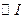 分别是
分别是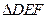 的外接圆和内切圆.
的外接圆和内切圆.
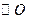 、
、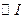 分别是
分别是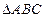 的外接圆和内切圆;证明:过
的外接圆和内切圆;证明:过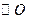 上的任意一点
上的任意一点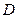 ,都可作一个三角形
,都可作一个三角形 ,使得
,使得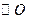 、
、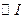 分别是
分别是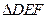 的外接圆和内切圆.
的外接圆和内切圆.略
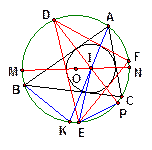
证:如图,设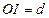 ,
,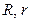 分别是
分别是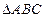 的外接圆和内切圆半径,延长
的外接圆和内切圆半径,延长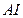 交
交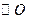 于
于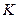 ,则
,则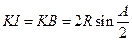 ,
,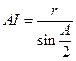 ,延长
,延长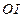 交
交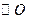 于
于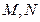 ;则
;则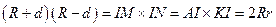 ,即
,即 ;
;
过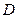 分别作
分别作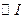 的切线
的切线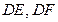 ,
,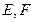 在
在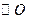 上,连
上,连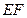 ,则
,则 平分
平分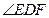 ,只要证,
,只要证,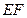 也与
也与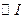 相切;
相切;
设 ,则
,则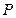 是
是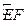 的中点,连
的中点,连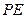 ,则
,则
 ,
,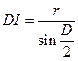 ,
,
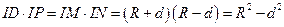 ,
,
所以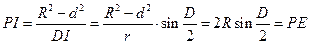 ,由于
,由于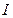 在角
在角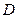 的平分线上,因此点
的平分线上,因此点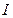 是
是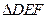 的内心,(这是由于,
的内心,(这是由于,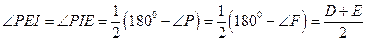 ,而
,而
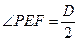 ,所以
,所以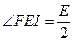 ,点
,点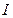 是
是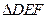 的内心).即弦
的内心).即弦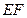 与
与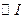 相切.
相切.
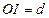 ,
,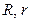 分别是
分别是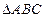 的外接圆和内切圆半径,延长
的外接圆和内切圆半径,延长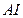 交
交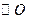 于
于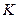 ,则
,则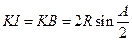 ,
,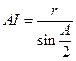 ,延长
,延长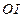 交
交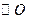 于
于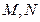 ;则
;则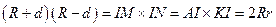 ,即
,即 ;
;
过
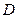 分别作
分别作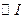 的切线
的切线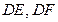 ,
,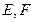 在
在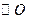 上,连
上,连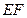 ,则
,则 平分
平分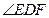 ,只要证,
,只要证,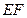 也与
也与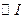 相切;
相切;设
 ,则
,则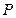 是
是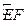 的中点,连
的中点,连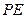 ,则
,则 ,
,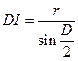 ,
,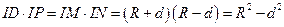 ,
,所以
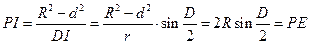 ,由于
,由于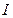 在角
在角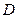 的平分线上,因此点
的平分线上,因此点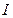 是
是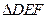 的内心,(这是由于,
的内心,(这是由于,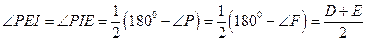 ,而
,而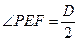 ,所以
,所以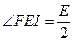 ,点
,点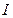 是
是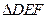 的内心).即弦
的内心).即弦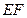 与
与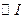 相切.
相切.
练习册系列答案
相关题目
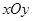 中,已知曲线
中,已知曲线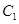 :
: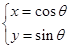 (
(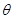 为参数),将
为参数),将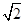 和
和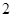 倍后得到曲线
倍后得到曲线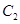 .以平面直角坐标系
.以平面直角坐标系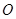 为极点,
为极点,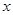 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线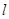 :
: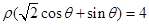 .
.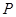 ,使点
,使点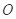 为极点,
为极点,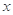 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点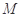 的极坐标为
的极坐标为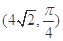 ,曲线
,曲线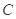 的参数方程为
的参数方程为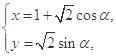 (
(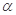 为参数).
为参数).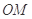 的直角坐标方程;
的直角坐标方程;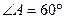 ,
,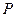 、
、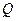 分别是
分别是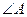 两边上的动点。
两边上的动点。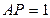 ,
,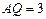 时,求
时,求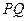 的长;
的长;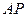 、
、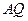 长度之和为定值4,求线段
长度之和为定值4,求线段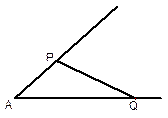
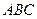 中,
中,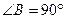 ,
,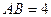 ,以
,以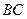 为直径的圆交
为直径的圆交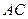 边于点
边于点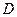 ,
,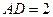 ,则
,则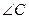 的大小为 .
的大小为 .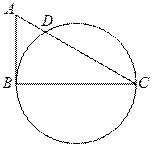
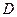 做圆的切线切于
做圆的切线切于 点,作割线交圆于
点,作割线交圆于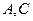 两点,其中
两点,其中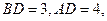
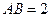 ,则
,则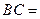

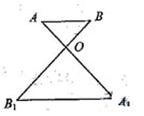
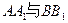 相交与点O,
相交与点O, 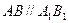 且
且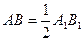 ,若
,若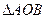 得外接圆直径为1,则
得外接圆直径为1,则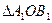 的外接圆直径为_________.
的外接圆直径为_________.