题目内容
在直角坐标平面内,以坐标原点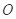 为极点,
为极点,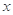 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点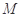 的极坐标为
的极坐标为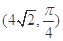 ,曲线
,曲线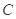 的参数方程为
的参数方程为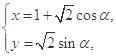 (
(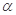 为参数).
为参数).
(1)求直线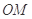 的直角坐标方程;
的直角坐标方程;
(2)求点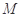 到曲线
到曲线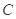 上的点的距离的最小值.
上的点的距离的最小值.
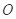 为极点,
为极点,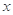 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点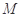 的极坐标为
的极坐标为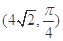 ,曲线
,曲线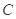 的参数方程为
的参数方程为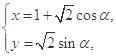 (
(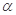 为参数).
为参数).(1)求直线
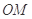 的直角坐标方程;
的直角坐标方程;(2)求点
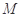 到曲线
到曲线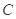 上的点的距离的最小值.
上的点的距离的最小值.(1)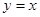 ;(2)
;(2)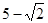 .
.
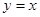 ;(2)
;(2)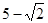 .
.试题分析:(1)将点
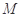 极坐标
极坐标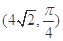 ,化为直角坐标,然后在直线坐标系中求直线
,化为直角坐标,然后在直线坐标系中求直线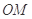 的方程;(2)由曲线
的方程;(2)由曲线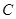 的参数方程化为普通方程为
的参数方程化为普通方程为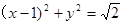 ,再数形结合考虑点
,再数形结合考虑点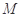 到曲线
到曲线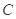 上的点的距离的最小值.
上的点的距离的最小值.试题解析:(1)∵点
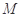 的极坐标为
的极坐标为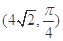 ,∴
,∴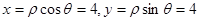 ,点
,点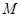 的直角坐标为
的直角坐标为(4,4),∴直线
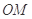 的直角坐标方程
的直角坐标方程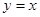 ;
;(2) 由曲线C的参数方程
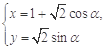 (
(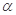 为参数),化成普通方程为:
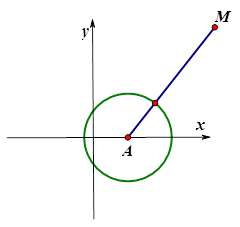
为参数),化成普通方程为: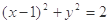 ,表示以
,表示以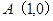 为圆心,半径为
为圆心,半径为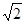 的圆,由于点
的圆,由于点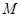 在曲线C外,故点M到曲线C上的点的距离最小值为
在曲线C外,故点M到曲线C上的点的距离最小值为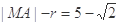 .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
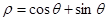 和直线
和直线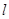 :
: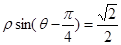 .
.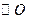 、
、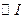 分别是
分别是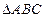 的外接圆和内切圆;证明:过
的外接圆和内切圆;证明:过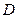 ,都可作一个三角形
,都可作一个三角形 ,使得
,使得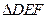 的外接圆和内切圆.
的外接圆和内切圆.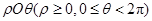 中,点
中,点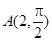 关于直线
关于直线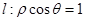 的对称点的极坐标为 .
的对称点的极坐标为 . 
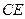 与⊙O的交点.若
与⊙O的交点.若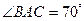 ,则
,则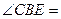 ______;若
______;若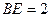 ,
,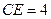 ,则
,则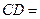 .
.
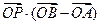 的值为______________
的值为______________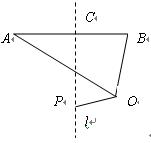
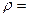 4sin(
4sin(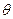 -
- )关于 ( )
)关于 ( )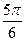 轴对称
轴对称 化为直角坐标方程 .
化为直角坐标方程 .