题目内容
【题目】教材中指出:当![]() 很小,
很小,![]() 不太大时,可以用
不太大时,可以用![]() 表示
表示![]() 的近似值,即
的近似值,即![]() (1),我们把近似值与实际值之差除以实际值的商的绝对值称为“相对近似误差”,一般用字母
(1),我们把近似值与实际值之差除以实际值的商的绝对值称为“相对近似误差”,一般用字母![]() 表示,即相对近似误差
表示,即相对近似误差![]()
(1)利用(1)求出![]() 的近似值,并指出其相对近似误差(相对近似误差保留两位有效数字)
的近似值,并指出其相对近似误差(相对近似误差保留两位有效数字)
(2)若利用(1)式计算![]() 的近似值产生的相对近似误差不超过
的近似值产生的相对近似误差不超过![]() ,求正实数
,求正实数![]() 的取值范围;
的取值范围;
(3)若利用(1)式计算![]() 的近似值产生的相对近似误差不超过
的近似值产生的相对近似误差不超过![]() ,求正整数
,求正整数![]() 的最大值。(参考对数数值:
的最大值。(参考对数数值:![]() )
)
【答案】(1)![]() ;
;![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据题意可求得近似值,由相对近似误差即可求得![]() 的值,并保留两位有效数字.
的值,并保留两位有效数字.
(2)根据题意,利用换元法可得关于![]() 的不等式组,解不等式即可求得正实数
的不等式组,解不等式即可求得正实数![]() 的取值范围;
的取值范围;
(3)根据定义可得关于![]() 的不等式,通过取对数化简,代入参考值即可求得正整数
的不等式,通过取对数化简,代入参考值即可求得正整数![]() 的最大值.
的最大值.
(1)由题意可知, 当![]() 很小,
很小,![]() 不太大时,可以用
不太大时,可以用![]() 表示
表示![]() 的近似值,即
的近似值,即![]()
所以近似值为![]()
相对近似误差![]()
所以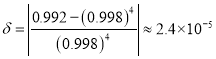
(2)令![]() ,则
,则![]()
由定义![]() 可知
可知![]()
由相对近似误差![]() 可知
可知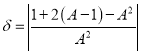
所以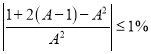
![]()
化简可得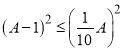
所以![]() ,即
,即![]()
所以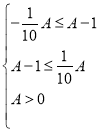 ,
,
解不等式组可得![]()
(3)由定义![]() 可知
可知![]()
由相对近似误差![]() 可知
可知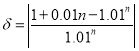
所以
化简可得![]()
等式两边同取对数可得![]()
当![]() 时,不等式左边等于
时,不等式左边等于![]() ,等式右边等于
,等式右边等于![]() ,不等式成立
,不等式成立
当![]() 时,不等式左边等于
时,不等式左边等于![]() ,等式右边等于
,等式右边等于![]() ,不等式不成立
,不等式不成立
综上可知, 正整数![]() 的最大值为
的最大值为![]()

 阅读快车系列答案
阅读快车系列答案【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.