题目内容
【题目】已知△ABC中,内角A,B,C的对边分别为a,b,c.
(1)若![]() ,且
,且![]() ,求角C大小;
,求角C大小;
(2)若△ABC为锐角三角形,且![]() ,求△ABC面积的取值范围.
,求△ABC面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先根据正弦定理,![]() ,代入后得到角的关系式
,代入后得到角的关系式![]() ,结合两角差的正弦公式得到
,结合两角差的正弦公式得到![]() ,然后根据三角形的内角和为
,然后根据三角形的内角和为![]() ,解得
,解得![]() ,代入后利用诱导公式和降幂公式:
,代入后利用诱导公式和降幂公式:![]() ,
,![]() ,解三角方程得到角C的值;
,解三角方程得到角C的值;
(2)根据正弦定理![]() 代入三角形的面积公式
代入三角形的面积公式![]() ,又
,又![]() ,化简为
,化简为![]() ,最后根据锐角三角形得到角B的取值范围,求得面积的取值范围.
,最后根据锐角三角形得到角B的取值范围,求得面积的取值范围.
试题解析:(1)由于![]() ,由正弦定理可得
,由正弦定理可得![]() ,
,
即sin(A-B)=0,∵A,B∈(0,π),∴A=B,故![]() ,
,
又![]() ,所以
,所以![]() ,
,
![]() ,
,
由于![]() ,所以cosC=0,由于C是三角形的内角,故
,所以cosC=0,由于C是三角形的内角,故![]() .
.
(2)由于![]() ,所以
,所以![]()
所以△ABC面积
![]() ,
,
由于△ABC为锐角三角形,所以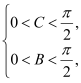 即
即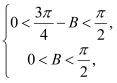
解得![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,
即△ABC面积的取值范围是![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目

