题目内容
【题目】在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在![]() 的平分线上.
的平分线上.

(1)求证:DE∥平面ABC;
(2)求此空间几何体的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)要证明线面平行,即先证明线线平行,取AC中点O,连接BO,DO,则BO⊥AC,DO⊥AC,作EF⊥平面ABC,根据题意,点F落在BO上,∴![]() EBF=60°,易求得
EBF=60°,易求得![]() ,这样就可证明
,这样就可证明![]() ,且
,且![]() ,所以四边形
,所以四边形![]() 是平行四边形,得到
是平行四边形,得到![]() ;(2)将几何体的体积分割为两个三棱锥的体积,即
;(2)将几何体的体积分割为两个三棱锥的体积,即![]() ,根据所给的数据代入得到结果.
,根据所给的数据代入得到结果.
试题解析:(1)由题意知,△ABC,△ACD都是边长为2的等边三角形,取AC中点O,连接BO,DO,则BO⊥AC,DO⊥AC,
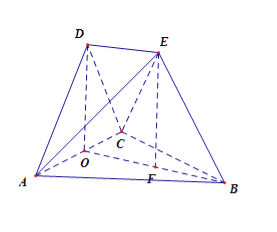
又∵平面ACD⊥平面ABC,∴DO⊥平面ABC,作EF⊥平面ABC,那么EF∥DO,根据题意,点F落在BO上,∴![]() EBF=60°,易求得
EBF=60°,易求得![]() ,
,
∴四边形DEFO是平行四边形,∴DE∥OF,DE![]() 平面ABC,OF
平面ABC,OF![]() 平面ABC,
平面ABC,
∴DE∥平面ABC.
(2)由(1):BO⊥AC,平面ACD⊥平面ABC且交线为AC,
∴BO⊥平面ACD,∴DE⊥平面ACD,
∴三棱锥E-ACD的体积
![]() ,
,
三棱锥E-ACB的体积![]() ,
,
∴此空间几何体的体积![]() .
.

练习册系列答案
相关题目

