题目内容
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有 恒成立,
恒成立,
则不等式 的解集是
的解集是
 恒成立,
恒成立,则不等式
 的解集是
的解集是| A.(-2,0) ∪(2,+∞) | B.(-2,0) ∪(0,2) | C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
D
本题考查函数的奇偶性,单调性,导数的运算,导数的应用,分类讨论的数学思想.
设函数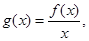 则
则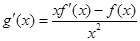 ;因为当
;因为当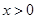 时,有
时,有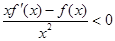 恒成立,即
恒成立,即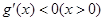 ,所以函数
,所以函数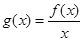 在
在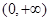 上是减函数;又因为
上是减函数;又因为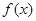 是奇函数,所以函数
是奇函数,所以函数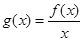 是偶函数;则
是偶函数;则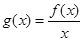 在
在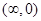 上是增函数;因为
上是增函数;因为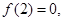 所以
所以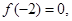 所以
所以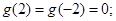 不等式
不等式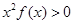 可化为
可化为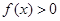 即
即
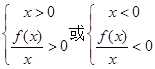 即
即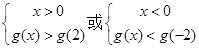 ,解得
,解得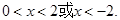
故选D
设函数
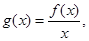 则
则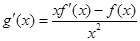 ;因为当
;因为当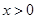 时,有
时,有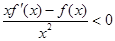 恒成立,即
恒成立,即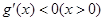 ,所以函数
,所以函数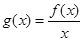 在
在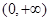 上是减函数;又因为
上是减函数;又因为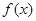 是奇函数,所以函数
是奇函数,所以函数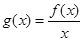 是偶函数;则
是偶函数;则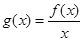 在
在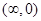 上是增函数;因为
上是增函数;因为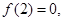 所以
所以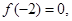 所以
所以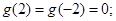 不等式
不等式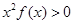 可化为
可化为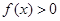 即
即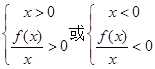 即
即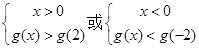 ,解得
,解得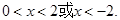
故选D

练习册系列答案
相关题目
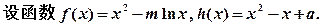
 时,
时,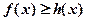 在
在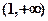 上恒成立,求实数
上恒成立,求实数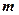 的取值范围;
的取值范围;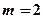 时,若函数
时,若函数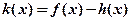 在
在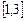 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数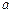 的取值范围;
的取值范围;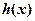 在公共定义域上具有相同的单调区间?若存在,求出
在公共定义域上具有相同的单调区间?若存在,求出 .
. 在区间[-3,4]
在区间[-3,4] 上的值域
上的值域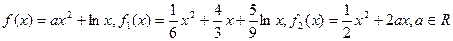 .
.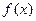 在点
在点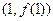 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;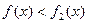 在区间
在区间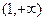 上恒成立,求
上恒成立,求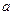 的取值范围;
的取值范围;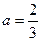 时,求证:在区间
时,求证:在区间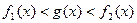 恒成立的函数
恒成立的函数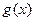
 是直线
是直线 上三点,向量
上三点,向量 满足:
满足: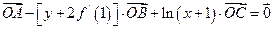 ,且函数
,且函数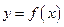 定义域内可导。
定义域内可导。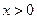 ,证明:
,证明: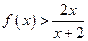 ;
;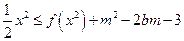 对
对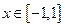 及
及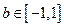 都恒成立,求实数
都恒成立,求实数 的取值范围。
的取值范围。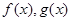 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当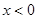 时,
时,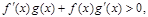 且
且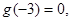 则不等式
则不等式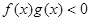 的解集是______________
的解集是______________ 是定义
是定义 在R上的奇函数,当
在R上的奇函数,当 时,
时, ,且
,且 ,
, 的解集为 ▲
的解集为 ▲ 
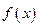 为定义在R上的偶函数,且导数
为定义在R上的偶函数,且导数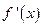 存在,则
存在,则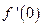 的值为 ( ▲ )
的值为 ( ▲ )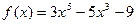 的极值点的个数( ▲ )
的极值点的个数( ▲ )