题目内容
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 ![]() 的中点.(12分)
的中点.(12分)
(Ⅰ)设P是 ![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.
【答案】解:(Ⅰ)∵AP⊥BE,AB⊥BE,且AB,AP平面ABP,AB∩AP=A,
∴BE⊥平面ABP,又BP平面ABP,
∴BE⊥BP,又∠EBC=120°,
因此∠CBP=30°;
(Ⅱ)解法一、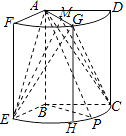
取 ![]() 的中点H,连接EH,GH,CH,
的中点H,连接EH,GH,CH,
∵∠EBC=120°,∴四边形BEGH为菱形,
∴AE=GE=AC=GC= ![]() .
.
取AG中点M,连接EM,CM,EC,
则EM⊥AG,CM⊥AG,
∴∠EMC为所求二面角的平面角.
又AM=1,∴EM=CM= ![]() .
.
在△BEC中,由于∠EBC=120°,
由余弦定理得:EC2=22+22﹣2×2×2×cos120°=12,
∴ ![]() ,因此△EMC为等边三角形,
,因此△EMC为等边三角形,
故所求的角为60°.
解法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.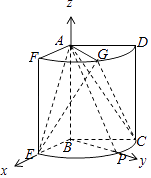
由题意得:A(0,0,3),E(2,0,0),G(1, ![]() ,3),C(﹣1,
,3),C(﹣1, ![]() ,0),
,0),
故 ![]() ,
, ![]() ,
, ![]() .
.
设 ![]() 为平面AEG的一个法向量,
为平面AEG的一个法向量,
由 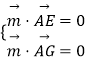 ,得
,得 ![]() ,取z1=2,得
,取z1=2,得 ![]() ;
;
设 ![]() 为平面ACG的一个法向量,
为平面ACG的一个法向量,
由 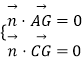 ,可得
,可得 ![]() ,取z2=﹣2,得
,取z2=﹣2,得 ![]() .
.
∴cos< ![]() >=
>= 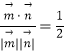 .
.
∴二面角E﹣AG﹣C的大小为60°.
【解析】(Ⅰ)由已知利用线面垂直的判定可得BE⊥平面ABP,得到BE⊥BP,结合∠EBC=120°求得∠CBP=30°;
(Ⅱ)法一、取 ![]() 的中点H,连接EH,GH,CH,可得四边形BEGH为菱形,取AG中点M,连接EM,CM,EC,得到EM⊥AG,CM⊥AG,说明∠EMC为所求二面角的平面角.求解三角形得二面角E﹣AG﹣C的大小.
的中点H,连接EH,GH,CH,可得四边形BEGH为菱形,取AG中点M,连接EM,CM,EC,得到EM⊥AG,CM⊥AG,说明∠EMC为所求二面角的平面角.求解三角形得二面角E﹣AG﹣C的大小.
法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.求出A,E,G,C的坐标,进一步求出平面AEG与平面ACG的一个法向量,由两法向量所成角的余弦值可得二面角E﹣AG﹣C的大小.
【考点精析】认真审题,首先需要了解旋转体(圆柱、圆锥、圆台)(常见的旋转体有:圆柱、圆锥、圆台、球),还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案

