Question

【题目】在平面直角坐标系xOy中，椭圆E： =1（a＞b＞0）的离心率为 ，焦距为2．（14分）
（Ⅰ）求椭圆E的方程．
（Ⅱ）如图，该直线l：y=k1x﹣ 交椭圆E于A，B两点，C是椭圆E上的一点，直线OC的斜率为k2 ， 且看k1k2= ，M是线段OC延长线上一点，且|MC|：|AB|=2：3，⊙M的半径为|MC|，OS，OT是⊙M的两条切线，切点分别为S，T，求∠SOT的最大值，并求取得最大值时直线l的斜率．

Answer 1

【答案】解：（Ⅰ）由题意知， ，解得a= ，b=1．
∴椭圆E的方程为 ；
（Ⅱ）设A（x1 ， y1），B（x2 ， y2），
联立 ，得 ．
由题意得△= ＞0．
， ．
∴|AB|= ．
由题意可知圆M的半径r为
r= ．
由题意设知， ，∴ ．
因此直线OC的方程为 ．
联立 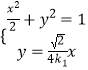，得 ．
因此，|OC|= ．
由题意可知，sin = ．
而 = ．
令t= ，则t＞1， ∈（0，1），
因此， = ≥1．
当且仅当 ，即t=2时等式成立，此时 ．
∴ ，因此 ．
∴∠SOT的最大值为 ．
综上所述：∠SOT的最大值为 ，取得最大值时直线l的斜率为 ．

【解析】（Ⅰ）由题意得关于a，b，c的方程组，求解方程组得a，b的值，则椭圆方程可求；
（Ⅱ）设A（x1 ， y1），B（x2 ， y2），联立直线方程与椭圆方程，利用根与系数的关系求得A，B的横坐标的和与积，由弦长公式求得|AB|，由题意可知圆M的半径r，则r= ．由题意设知 ．得到直线OC的方程，与椭圆方程联立，求得C点坐标，可得|OC|，由题意可知，sin = ．转化为关于k1的函数，换元后利用配方法求得∠SOT的最大值为 ，取得最大值时直线l的斜率为 ．
【考点精析】本题主要考查了函数的值域和椭圆的标准方程的相关知识点，需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的；椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．