题目内容
11.在△ABC中,AB=BC,∠B=90°,M为BC的中点,BN⊥AM,且交AC于点N,用解析法证明:∠CMN=∠BMA.分析 以B为原点,BC为x轴,BA为y轴建立平面直角坐标系,设A坐标(0,2),则B坐标(2,0),M坐标(1,0),画出相应的图象,分别求出直线AM,AC,BN的直线方程,求出点N的坐标,根据三角函数值即可证明.
解答 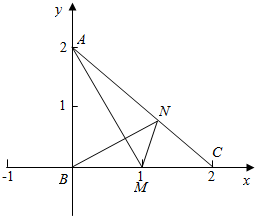 证明:以B为原点,BC为x轴,BA为y轴建立平面直角坐标系,
证明:以B为原点,BC为x轴,BA为y轴建立平面直角坐标系,
设A坐标(0,2),则B坐标(2,0),M坐标(1,0),
设直线AM方程为y=kx+b,把A、M代入得:y=-2x+2,
同样解得AC方程为y=-x+2,
∵BN⊥AM,
∴直线BN的斜率为$\frac{1}{2}$且过原点,即BN方程为y=$\frac{1}{2}$x,
联立AC和BN得方程组$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{1}{2}x}\end{array}\right.$,
解得点N坐标为($\frac{4}{3}$,$\frac{2}{3}$),
tanCMN=$\frac{\frac{4}{3}}{\frac{2}{3}}$=2,tanBMA=$\frac{2}{1}$=2,
∴∠CMN=∠BMA.
点评 本题借助于平面直角坐标系,利用解析法证明角相等的问题,关键是建立坐标系,构造点的坐标,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
1.己知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,O为原点,在椭圆上存在一个点P使得△OFP为等边三角形,则椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | 2-$\sqrt{3}$ | C. | $\frac{{\sqrt{5}}}{2}-1$ | D. | $\frac{{\sqrt{5}}}{2}-1$ |