题目内容
若实数x、y、m满足|x-m|<|y-m|,则称x比y接近m。
(I)若x2-1比3接近0,求x的取值范围;
(Ⅱ)对任意两个不相等的正数a、b,证明:a2b+ab2比a3+b3接近2ab ;
;
(Ⅲ)已知函数f(x)的定义域D={x|x≠kπ,k∈Z,x∈R}。任取x∈D,f(x)等于1+sinx和1-sinx中接近0的那个值。写出函数f(x)的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明)。
(I)若x2-1比3接近0,求x的取值范围;
(Ⅱ)对任意两个不相等的正数a、b,证明:a2b+ab2比a3+b3接近2ab
 ;
;(Ⅲ)已知函数f(x)的定义域D={x|x≠kπ,k∈Z,x∈R}。任取x∈D,f(x)等于1+sinx和1-sinx中接近0的那个值。写出函数f(x)的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明)。
解:(Ⅰ)由题意得|x2-1|<3,即-3<x2-1<3
解得-2<x<2
∴x的取值范围是(-2,2);
(Ⅱ)证明:当a、b是不相等的正数时,a3+b3-(a2b+ab2)=(a-b)2(a+b)>0
又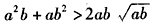
则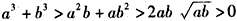
于是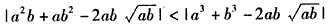
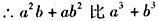 接近
接近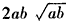 ;
;
(Ⅲ)由|1-sinx|< |1+sinx|得1-sinx<1+sinx,即sinx>0,则2kπ<x<2kπ+π(k∈Z)
同理,若|1+sinx|< |1-sinx|,则2kπ+π<x<2kπ +2π(k∈Z)
于是,函数f(x)的解析式是
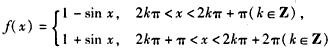
函数f(x)的大致图象如下:
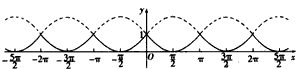
函数f(x)的最小正周期T=π
函数f(x)是偶函数
当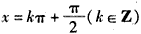 时,函数f(x)取得最小值0
时,函数f(x)取得最小值0
函数f(x)在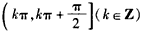 上单调递减;
上单调递减;
在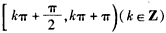 上单调递增。
上单调递增。
解得-2<x<2
∴x的取值范围是(-2,2);
(Ⅱ)证明:当a、b是不相等的正数时,a3+b3-(a2b+ab2)=(a-b)2(a+b)>0
又
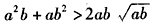
则
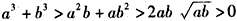
于是
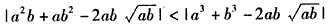
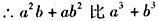 接近
接近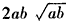 ;
;(Ⅲ)由|1-sinx|< |1+sinx|得1-sinx<1+sinx,即sinx>0,则2kπ<x<2kπ+π(k∈Z)
同理,若|1+sinx|< |1-sinx|,则2kπ+π<x<2kπ +2π(k∈Z)
于是,函数f(x)的解析式是
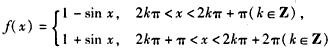
函数f(x)的大致图象如下:

函数f(x)的最小正周期T=π
函数f(x)是偶函数
当
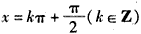 时,函数f(x)取得最小值0
时,函数f(x)取得最小值0函数f(x)在
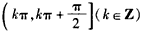 上单调递减;
上单调递减;在
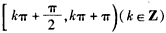 上单调递增。
上单调递增。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目