题目内容
已知椭圆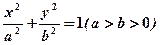
的离心率
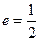，过左焦点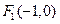
的直线交椭圆于
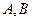两点，椭圆的右焦点为
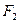，则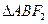
的周长是 ﹡ ．则可以输出的函数是 ﹡ ．
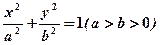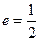的离心率，过左焦点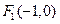的直线交椭圆于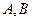两点，椭圆的右焦点为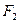，则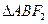的周长是 ﹡ ．则可以输出的函数是 ﹡ ．8 3
略
练习册系列答案
相关题目
题目内容
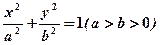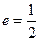的离心率，过左焦点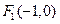的直线交椭圆于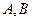两点，椭圆的右焦点为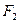，则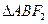的周长是 ﹡ ．则可以输出的函数是 ﹡ ．
的左右焦点分别为F1、F2，点P在椭圆C上，且PF1⊥F1F2, |PF1|=
, |PF2|=
. 
的圆心M交椭圆于A、B两点，且A、B关于点M对称，求直线L的方程。
的左焦点为
，上顶点为
，过点
垂直的直线分别交椭圆
与
轴正半轴于点
，且
. ⑴求椭圆
、
相切，求椭圆
中，如图，已知椭圆
的左右顶点为A,B，右顶点为F，设过点T（
）的直线TA,TB与椭圆分别交于点M
，
，其中m>0,
,求点P的轨迹
，求点T的坐标
,求证：直线MN必过x轴上的一定点
，且椭圆过点（2，0）。
上的点到椭圆C上点的距离的最大值与最小值。
给出下面四个命题：
时，曲线C表示椭圆；
或
轴上的椭圆，则
的焦点坐标为（ ）
）和（0，—
上任一点，F1、F2为椭圆的两焦点，若
则
的右焦点F为圆心，a为半径的圆与椭圆的右准线交于不同的两点，则该椭圆的离心率的取值范围是 （ ）
