题目内容
15.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(-2,0)若$\overrightarrow{c}$⊥$\overrightarrow{b}$($\overrightarrow{c}$≠$\overrightarrow{0}$),当t∈[-$\sqrt{3}$,2]时,|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|的取值范围为[1,$\sqrt{13}$].分析 由已知求出$\overrightarrow{c}$用t表示的坐标,得到t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$的坐标,然后用t表示|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|,根据t∈[-$\sqrt{3}$,2]求其范围.
解答 解:由已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(-2,0)若$\overrightarrow{c}$⊥$\overrightarrow{b}$($\overrightarrow{c}$≠$\overrightarrow{0}$),设$\overrightarrow{c}$=(x,y),则-2x+0=0,即x=0,所以$\overrightarrow{c}$=(0,y),则t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$=(0,t),
所以$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$=(1,$\sqrt{3}$-t),
所以,|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|2=1+($\sqrt{3}$-t)2,又t∈[-$\sqrt{3}$,2],
所以当t=$\sqrt{3}$时,|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|2的最小值为1;当t=$-\sqrt{3}$时,|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|2的最大值为13;
所以|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|的取值范围为[1,$\sqrt{13}$];
故答案为:[1,$\sqrt{13}$].
点评 本题考查了向量的加减法的坐标运算以及向量模的求法.

 阅读快车系列答案
阅读快车系列答案| A. | $f({-\frac{1}{2}})<f({\frac{3}{4}})<f({\frac{2}{3}})$ | B. | $f({-\frac{1}{2}})<f({\frac{2}{3}})<f({\frac{3}{4}})$ | C. | $f({\frac{3}{4}})<f({\frac{2}{3}})<f({-\frac{1}{2}})$ | D. | $f({\frac{2}{3}})<f({-\frac{1}{2}})<f({\frac{3}{4}})$ |
(Ⅰ)求数列{a2,n}的通项公式;
(Ⅱ)设bn=$\frac{1}{{{a_{n,}}_1{a_{n+2,1}}}}+{(-1)^n}{a_{n,1}}$,求数列{bn}的前n和Sn.
| a1,1 | a1,2 | a1,3 | a1,4 | … |
| a2,1 | a2,2 | a2,3 | a2,4 | … |
| a3,1 | a3,2 | a3,3 | a3,4 | … |
| a4,1 | a4,2 | a4,3 | a4,4 | … |
| … | … | … | … | … |
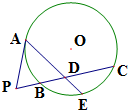 如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明:AD•DE=2PB2.
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明:AD•DE=2PB2.