题目内容
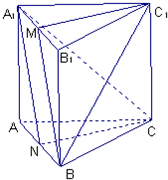
正三棱柱ABC-A1B1C1中,M、N分别为A1B1、AB的中点.
①求证:平面A1NC∥平面BMC1;
②若AB=AA1,求BM与AC所成角的余弦值.
①求证:平面A1NC∥平面BMC1;
②若AB=AA1,求BM与AC所成角的余弦值.

①证明:在正三棱柱ABC-A1B1C1中,M、N分别为A1B1、AB的中点,
所以A1N∥BM,
因为BM?平面BMC1,A1N?平面BMC1,
所以A1N∥平面BMC1.
因为M、N分别为A1B1、AB的中点,
所以C1M∥CN,
因为C1M?平面BMC1,CN?平面BMC1,
所以CN∥平面BMC1.
又因为CN∩A1N=N,并且CN?平面A1NC,A1N?平面A1NC
所以平面A1NC∥平面BMC1.
②由 ①可得A1N∥BM,
又因为AC∥A1C1,
所以BM与AC所成角等于A1C1与A1N所成的角,
即∠NA1C1为所求或者与其互补.
连接C1N,在△NA1C1中,设AB=AA1=2,所以A1N=
,A1C1=2,NC1=
,
所以根据余弦定理可得:cosNA1C1=
.
所以BM与AC所成角的余弦值
.
所以A1N∥BM,
因为BM?平面BMC1,A1N?平面BMC1,
所以A1N∥平面BMC1.
因为M、N分别为A1B1、AB的中点,
所以C1M∥CN,
因为C1M?平面BMC1,CN?平面BMC1,
所以CN∥平面BMC1.
又因为CN∩A1N=N,并且CN?平面A1NC,A1N?平面A1NC
所以平面A1NC∥平面BMC1.
②由 ①可得A1N∥BM,
又因为AC∥A1C1,
所以BM与AC所成角等于A1C1与A1N所成的角,
即∠NA1C1为所求或者与其互补.
连接C1N,在△NA1C1中,设AB=AA1=2,所以A1N=
| 5 |
| 7 |
所以根据余弦定理可得:cosNA1C1=
| ||
| 10 |
所以BM与AC所成角的余弦值
| ||
| 10 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目