题目内容
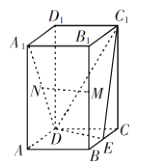
【题目】已知四棱锥
中，
平面ABCD，
，
，
，M是线段AB的中点.
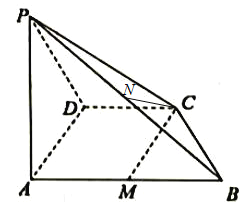
（1）求证：
平面PAB；
（2）已知点N是线段PB的中点，试判断直线CN与平面PAD的位置关系，并证明你的判断.
【答案】（1）证明见解析（2）
平面PAD；证明见解析
【解析】
（1）证明
，
，即得
平面PAB；（2）判断平面PAD，取线段PA的中点F，连结FN，DF，证明
，平面PAD即得证.
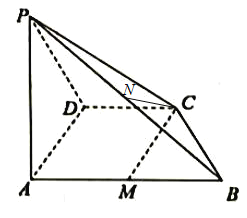
（1）∵
，
，
∴
是等边三角形，M是线段AB的中点
∴，
又∵
平面ABCD，
平面ABCD，
∴，
又∵
，
平面PAB
∴平面PAB.
（2）判断平面PAD.
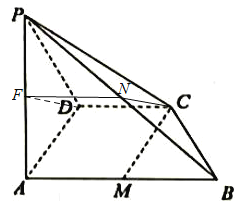
证明：取线段PA的中点F，连结FN，DF，
∴
，
∵M是线段AB的中点，
，
∴
，
∴CDPN是平行四边形，
∴，
又∵
平面PAD，
平面PAD，
∴平面PAD.
阅读快车系列答案
【题目】为了研究某学科成绩是否与学生性别有关，采用分层抽样的方法，从高三年级抽取了30名男生和20名女生的该学科成绩，得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图，规定80分以上为优分（含80分）．
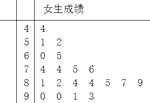
（Ⅰ）（i）请根据图示，将2×2列联表补充完整；
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
（ii）据此列联表判断，能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”？
（Ⅱ）将频率视作概率，从高三年级该学科成绩中任意抽取3名学生的成绩，求至少2名学生的成绩为优分的概率．
附：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
．
【题目】辽宁号航母纪念章从2012年10月5日起开始上市，通过市场调查，得到该纪念章每1枚的市场价y（单位：元）与上市时间x（单位：天）的数据如下：
上市时间x天 | 8 | 10 | 32 |
市场价y元 | 82 | 60 | 82 |
（1）根据上表数据，从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价y与上市时间x的变化关系并说明理由：①
；②
；③
.
（2）利用你选取的函数，求辽宁号航母纪念章市场价最低时的上市天数及最低的价格.
