题目内容
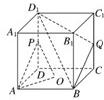10、如图，在正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO？分析：首先确定当Q为CC1的中点时，平面D1BQ∥平面PAO，证明QB∥PA，进而证明QB∥面PAO，再利用三角形的中位线的性质证明
D1B∥PO，进而证明D1B∥面PAO，这样，在平面D1BQ中有2条相交直线D1B、QB平行于平面PAO，故有平面D1BQ∥平面PAO．
D1B∥PO，进而证明D1B∥面PAO，这样，在平面D1BQ中有2条相交直线D1B、QB平行于平面PAO，故有平面D1BQ∥平面PAO．
解答：解：当Q为CC1的中点时，平面D1BQ∥平面PAO．
∵Q为CC1的中点，P为DD1的中点，∴QB∥PA．
连接DB．∵P、O分别为DD1、DB的中点，
∴D1B∥PO．又D1B?平面PAO，QB?平面PAO，
∴D1B∥面PAO，QB∥面PAO，
又D1B∩QB=B，
∴平面D1BQ∥平面PAO．
∵Q为CC1的中点，P为DD1的中点，∴QB∥PA．
连接DB．∵P、O分别为DD1、DB的中点，
∴D1B∥PO．又D1B?平面PAO，QB?平面PAO，
∴D1B∥面PAO，QB∥面PAO，
又D1B∩QB=B，
∴平面D1BQ∥平面PAO．
点评：本题考查平面与平面平行的一般方法，即在一个平面内找到2条相交直线和另一个平面平行．
练习册系列答案
相关题目
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体的一角上截取三棱锥P-ABC，PO为棱锥的高，记
若Rt△ABC中两直角边为a、b，斜边c上的高为h，则
如图，在正方体ABCD-A1B1C1D1中，E为DD1的中点，
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-ABC的主视图与左视图的面积的比值为（ ）