题目内容
【题目】已知长为2的线段A B两端点A和B分别在x轴和y轴上滑动，线段AB的中点M的轨迹为曲线C． （Ⅰ）求曲线C的方程；
（Ⅱ）点P（x，y）是曲线C上的动点，求3x﹣4y的取值范围；
（Ⅲ）已知定点Q（0， 
），探究是否存在定点T（0，t）（t 
）和常数λ满足：对曲线C上任意一点S，都有|ST|=λ|SQ|成立？若存在，求出t和λ；若不存在，请说明理由．
【答案】解：（Ⅰ）法一：设A（m，0），B（0，n），M（x，y），则|AB|2=m2+n2① ∵点M为线段AB的中点∴m=2x，n=2y；代入①式得4x2+4y2=4，
即点M的轨迹曲线C的方程为x2+y2=1．
法二：设O为坐标原点，则 
，故点M的轨迹曲线C是以原点O为圆心，
半径等于1的圆，其方程为x2+y2=1．
（Ⅱ）法一；∵x2+y2=1，∴可令 
，∴3x﹣4y=3cosθ﹣4sinθ=5sin（θ+φ）∈[﹣5，5]．
法二：设t=3x﹣4y，则由题直线3x﹣4y﹣t=0与圆C：x2+y2=1有公共点，
∴ 
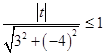，解得t∈[﹣5，5]
（Ⅲ）假设存在满足题意的t和λ，则设S（x，y），由|ST|=λ|SQ|得：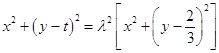 
，展开整理得： 
，又x2+y2=1，故有 
，
由题意此式对满足x2+y2=1的任意的y都成立，
∴ 
且 
，解得： 
（∵ 
）
所以存在 满足题意要求
【解析】（Ⅰ）法一：设A（m，0），B（0，n），M（x，y），利用|AB|2=m2+n2 ， 以及点M为线段AB的中点求解点M的轨迹曲线C的方程． 法二：设O为坐标原点，则 
，判断点M的轨迹曲线C是以原点O为圆心，半径等于1的圆，写出方程即可．（Ⅱ）法一；通过x2+y2=1，令 
，转化三角函数求解最值即可．法二：设t=3x﹣4y，利用直线3x﹣4y﹣t=0与圆C：x2+y2=1有公共点，列出不等式求解即可．（Ⅲ）假设存在满足题意的t和λ，则设S（x，y），由|ST|=λ|SQ|得： 
，化简代入x2+y2=1，推出 
，推出 
，得到结果．
