题目内容
【题目】已知数列{an}的前n项和为Sn ， 满足Sn= 
an﹣n（t＞0且t≠1，n∈N*）
（1）证明：数列{an+1}为等比数列，并求数列{an}的通项公式（用t，n表示）
（2）当t=2时，令cn= 
，证明 
≤c1+c2+c3+…+cn＜1．
【答案】
（1）证明：∵数列{an}的前n项和为Sn，满足Sn= 
an﹣n（t＞0且t≠1，n∈N*），
∴由题意当n=1时，a1=t﹣1，
∵Sn= an﹣n，①
∴Sn+1= an+1﹣（n+1），②
②﹣①得an+1=tan+t﹣1，即an+1+1=t（an+1），
∴{an+1}是以t为首项，以t为公比的等比数列
∴数列{an}的通项公式 
（2）证明： 
= 
= 
令Tn=c1+c2+c3+…+cn，
则Tn=（1﹣ 
）+（ 
）+（ 
）+…+（ ）=1﹣ 
．
∵Tn单调递增，∴当n=1时，（Tn）min= 
，当n趋向无穷大时，Tn趋近1．
∴ ≤c1+c2+c3+…+cn＜1
【解析】（1）当n=1时，a1=t﹣1，an+1+1=t（an+1），由此能证明{an+1}是以t为首项，以t为公比的等比数列，并能求出数列{an}的通项公式．（2） 
= ，利用裂项求和法求出Tn=c1+c2+c3+…+cn=1﹣ ，由此能证明 ≤c1+c2+c3+…+cn＜1．
【考点精析】通过灵活运用等比数列的通项公式（及其变式），掌握通项公式：
即可以解答此题．
【题目】为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
（Ⅰ）求y关于x的线性回归方程 
；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式： 
= 
= 
， 
．
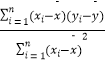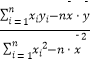