题目内容
7.若数列{an}满足a1=1,an+1=2nan,则数列{an}的通项公式an=${2}^{\frac{n(n-1)}{2}}$.分析 通过对an+1=2nan变形可知$\frac{{a}_{n+1}}{{a}_{n}}$=2n,进而利用累乘法计算可得结论.
解答 解:∵an+1=2nan,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=2n,
∴$\frac{{a}_{n}}{{a}_{n-1}}={2}^{n-1}$,$\frac{{a}_{n-1}}{{a}_{n-2}}={2}^{n-2}$,…,$\frac{{a}_{2}}{{a}_{1}}={2}^{1}$,
累乘得:$\frac{{a}_{n}}{{a}_{1}}$=21+2+3+…+(n-1)=${2}^{\frac{n(n-1)}{2}}$(n≥2),
∴an=${2}^{\frac{n(n-1)}{2}}$(n≥2),
又∵a1=1满足上式,
∴an=${2}^{\frac{n(n-1)}{2}}$,
故答案为:an=${2}^{\frac{n(n-1)}{2}}$.
点评 本题考查数列的通项,利用累乘法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.函数f(x)=ax(a>0,且a≠1),若f(3a)>$\sqrt{a}$,则实数a的取值范围为( )
| A. | (0,$\frac{1}{2}$)∪(1,+∞) | B. | (0,$\frac{1}{2}$)∪(1,2) | C. | (0,$\frac{1}{6}$)∪(1,+∞) | D. | (0,$\frac{1}{6}$)∪(1,6) |
4.已知函数f(x-$\frac{π}{6}$)=sin2x,则f($\frac{π}{2}$)等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
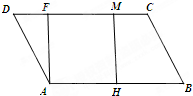 如图,在平行四边形ABCD中,AH=HB,DF=MC=$\frac{1}{4}$DC,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a,\overrightarrow b$分别表示$\overrightarrow{AM},\overrightarrow{MH},\overrightarrow{AF}$.
如图,在平行四边形ABCD中,AH=HB,DF=MC=$\frac{1}{4}$DC,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a,\overrightarrow b$分别表示$\overrightarrow{AM},\overrightarrow{MH},\overrightarrow{AF}$.