��Ŀ����
��2012•ͨ����һģ����������{an}���ӵڶ�����ÿһ������ǰһ��IJ�������ɵȱ����У��Ƹõȱ�����Ϊ����{an}�ġ���ȱ����С�����Ϊ����{bn}��������{bn}������b1=2������Ϊq��qΪ��������
��I����q=2��д��һ������{an}��ǰ4�
��II���������ж�����{an}�Ƿ�Ϊ�Ȳ����У���˵��������ɣ�
������a1��q����ʲô����������{an}�ǵȱ����У���֤����Ľ��ۣ�
��III����a1=1��1��q��2������{an+cn}�ǹ���Ϊq�ĵȲ����У�n��N*������c1=q����ʹ��cn��0������n��ȡֵ��Χ��
��I����q=2��д��һ������{an}��ǰ4�
��II���������ж�����{an}�Ƿ�Ϊ�Ȳ����У���˵��������ɣ�
������a1��q����ʲô����������{an}�ǵȱ����У���֤����Ľ��ۣ�
��III����a1=1��1��q��2������{an+cn}�ǹ���Ϊq�ĵȲ����У�n��N*������c1=q����ʹ��cn��0������n��ȡֵ��Χ��
������������Ϊ����{bn}�ǵȱ����У���b1=2��q=2������b2=4��b3=8���ɴ��ܹ����һ������{an}��ǰ4�
����������Ϊb1=2������an-a1=2(1+q+q2+��+qn-2)��q=1ʱ������{an}�ǵȲ����У���q��1ʱ������{an}���ǵȲ����У�
��������Ϊ����{bn}�ǵȱ����У�����b1=2������Ϊq������b2=2q��b3=2q2������a2=a1+2��a3=a1+2+2q����Ϊ����{an}�ǵȱ����У�����a22=a1•a3�����Ե�q=
ʱ������{an}�ǵȱ����У�
������Ϊ{an+cn}�ǹ���Ϊq�ĵȲ����У����ԣ�an+cn��-��an-1+cn-1��=q���ɴ˲��룺��n��3ʱ��cn��0��������ѧ���ɷ�֤����
����������Ϊb1=2������an-a1=2(1+q+q2+��+qn-2)��q=1ʱ������{an}�ǵȲ����У���q��1ʱ������{an}���ǵȲ����У�
��������Ϊ����{bn}�ǵȱ����У�����b1=2������Ϊq������b2=2q��b3=2q2������a2=a1+2��a3=a1+2+2q����Ϊ����{an}�ǵȱ����У�����a22=a1•a3�����Ե�q=
| a1+2 |
| a1 |
������Ϊ{an+cn}�ǹ���Ϊq�ĵȲ����У����ԣ�an+cn��-��an-1+cn-1��=q���ɴ˲��룺��n��3ʱ��cn��0��������ѧ���ɷ�֤����
����⣺������Ϊ����{bn}�ǵȱ����У���b1=2��q=2��
����b2=4��b3=8��
����a1=1��a2=3��a3=7��a4=15����д������������һ�鼴�ɣ�
����2�֣�
����������Ϊb1=2��
����a2-a1=2��a3-a2=2q��a4-a3=2q2������an-an-1=2qn-2��n��2��
����an-a1=2(1+q+q2+��+qn-2)��
����q=1������an-an-1=2��
��������{an}�ǵȲ����У�����3�֣�
����q��1������an=
+a1��
����an+1-an=
-
=
=2qn-1��
��Ϊq��1������2qn-1���dz�����
��������{an}���ǵȲ����У�����5�֣�
��������Ϊ����{bn}�ǵȱ����У�����b1=2������Ϊq��
����b2=2q��b3=2q2������a2=a1+2��a3=a1+2+2q��
��Ϊ����{an}�ǵȱ����У�
����a22=a1•a3��
����a1+2��2=a1•��a1+2+2q����
����q=
��
���Ե�q=
ʱ������{an}�ǵȱ����У�����7�֣�
������Ϊ{an+cn}�ǹ���Ϊq�ĵȲ����У�
���ԣ�an+cn��-��an-1+cn-1��=q��
��an-an-1=2qn-2��
����cn-cn-1=q-2qn-2��
����cn-1-cn-2=q-2qn-3������c3-c2=q-2q��c2-c1=q-2��
����cn=nq-2(qn-2+qn-3+��+q+1��
=nq-
������9�֣�
����c1=q��0��c2=2��q-1����0��c3=q-2��0��
c4=-2��q2-q+1��=-2��q-
��2-
��0����
���룺��n��3ʱ��cn��0��
����ѧ���ɷ�֤����
�ٵ�n=3ʱ��c3��0��Ȼ������
�ڼ��赱n=k��k��3��ʱ��ck��0��
��ô��n=k+1ʱ��cn+1=cn+q-2qn-1��q-2qk-1=q��1-2qk-2����
��Ϊ1��q��2��k��3��
����1-2qk-2��0��
����cn+1��0��
���Ե�n=k+1ʱ��cn+1��0������
�ɢ١�����������n��3ʱ������cn��0������14�֣�
����b2=4��b3=8��
����a1=1��a2=3��a3=7��a4=15����д������������һ�鼴�ɣ�
����2�֣�
����������Ϊb1=2��
����a2-a1=2��a3-a2=2q��a4-a3=2q2������an-an-1=2qn-2��n��2��
����an-a1=2(1+q+q2+��+qn-2)��
����q=1������an-an-1=2��
��������{an}�ǵȲ����У�����3�֣�
����q��1������an=
| 2(1-qn-1) |
| 1-q |
����an+1-an=
| 2(1-qn) |
| 1-q |
| 2(1-qn-1) |
| 1-q |
| 2qn-1-2qn |
| 1-q |
��Ϊq��1������2qn-1���dz�����
��������{an}���ǵȲ����У�����5�֣�
��������Ϊ����{bn}�ǵȱ����У�����b1=2������Ϊq��
����b2=2q��b3=2q2������a2=a1+2��a3=a1+2+2q��
��Ϊ����{an}�ǵȱ����У�
����a22=a1•a3��
����a1+2��2=a1•��a1+2+2q����
����q=
| a1+2 |
| a1 |
���Ե�q=
| a1+2 |
| a1 |
������Ϊ{an+cn}�ǹ���Ϊq�ĵȲ����У�
���ԣ�an+cn��-��an-1+cn-1��=q��
��an-an-1=2qn-2��
����cn-cn-1=q-2qn-2��
����cn-1-cn-2=q-2qn-3������c3-c2=q-2q��c2-c1=q-2��
����cn=nq-2(qn-2+qn-3+��+q+1��
=nq-
| 2(1-qn-1) |
| 1-q |
����c1=q��0��c2=2��q-1����0��c3=q-2��0��
c4=-2��q2-q+1��=-2��q-
| 1 |
| 2 |
| 3 |
| 2 |
���룺��n��3ʱ��cn��0��
����ѧ���ɷ�֤����
�ٵ�n=3ʱ��c3��0��Ȼ������
�ڼ��赱n=k��k��3��ʱ��ck��0��
��ô��n=k+1ʱ��cn+1=cn+q-2qn-1��q-2qk-1=q��1-2qk-2����
��Ϊ1��q��2��k��3��
����1-2qk-2��0��
����cn+1��0��
���Ե�n=k+1ʱ��cn+1��0������
�ɢ١�����������n��3ʱ������cn��0������14�֣�
���������⿼��Ȳ����к͵ȱ����е�֤�����ۺ���ǿ���Ѷȴ���ѧ˼ά��Ҫ��ϸߣ�����ʱҪ�������⣬��ϸ���ע����ѧ���ɷ��ĺ������ã�

��ϰ��ϵ�д�
 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
�����Ŀ
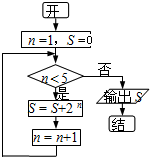 ��2012•ͨ����һģ����ͼ�������ͼ�����е���������ǣ�������
��2012•ͨ����һģ����ͼ�������ͼ�����е���������ǣ�������