题目内容
(2012•通州区一模)已知函数f(x)=lnx-x2.
(I)求函数f(x)的单调递增区间;
(II)求函数f(x)在(0,a](a>0)上的最大值.
(I)求函数f(x)的单调递增区间;
(II)求函数f(x)在(0,a](a>0)上的最大值.
分析:(Ⅰ)求导函数,令f′(x)>0,可得函数f(x)的单调递增区;
(Ⅱ)由(Ⅰ)知函数在(0,
)为增函数,同理可得函数f(x)在(
,+∞)为减函数,进而分类讨论,确定函数f(x)在(0,a](a>0)上的单调性,从而可求函数f(x)最大值.
(Ⅱ)由(Ⅰ)知函数在(0,
| ||
| 2 |
| ||
| 2 |
解答:解:(Ⅰ)因为函数f(x)=lnx-x2,x>0,所以f′(x)=
-2x=
令f′(x)>0,所以0<x<
所以函数f(x)的单调递增区间是(0,
).…(5分)
(Ⅱ)由(Ⅰ)知函数在(0,
)为增函数,
同理可得函数f(x)在(
,+∞)为减函数.…(6分)
所以当0<a<
时,函数f(x)在(0,a)上单调递增,
所以函数f(x)的最大值为f(a)=lna-a2; …(9分)
当a≥
时,函数f(x)在(0,
)上单调递增,在(
,a)上单调递减,
所以函数f(x)最大值为f(
)=ln
-
…(12分)
综上所述,当0<a<
时,函数f(x)的最大值为f(a)=lna-a2; 当a≥
时,函数f(x)最大值为f(
)=ln
-
…(13分)
| 1 |
| x |
| 1-2x2 |
| x |
令f′(x)>0,所以0<x<
| ||
| 2 |
所以函数f(x)的单调递增区间是(0,
| ||
| 2 |
(Ⅱ)由(Ⅰ)知函数在(0,
| ||
| 2 |
同理可得函数f(x)在(
| ||
| 2 |
所以当0<a<
| ||
| 2 |
所以函数f(x)的最大值为f(a)=lna-a2; …(9分)
当a≥
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
所以函数f(x)最大值为f(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
综上所述,当0<a<
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查函数的单调性,考查函数的最值,正确求导,确定函数的单调性是关键.

练习册系列答案
相关题目
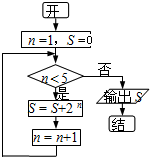 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )