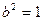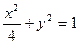题目内容
设椭圆的中心在原点,焦点在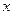 轴上,离心率
轴上,离心率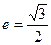 .已知点
.已知点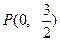 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为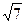 ,求这个椭圆方程.
,求这个椭圆方程.
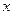 轴上,离心率
轴上,离心率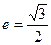 .已知点
.已知点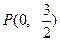 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为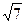 ,求这个椭圆方程.
,求这个椭圆方程.设椭圆方程为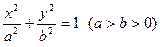 ,
, 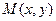 为椭圆上的点,由
为椭圆上的点,由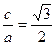 得
得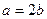
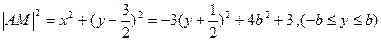
若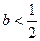 ,则当
,则当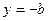 时
时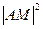 最大,即
最大,即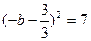 ,
, 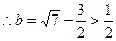 ,故矛盾.
,故矛盾.
若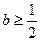 时,
时,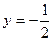 时
时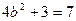 ,
, 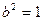
所求方程为
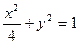
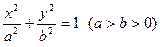 ,
, 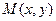 为椭圆上的点,由
为椭圆上的点,由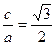 得
得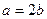
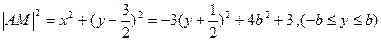
若
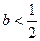 ,则当
,则当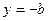 时
时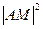 最大,即
最大,即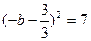 ,
, 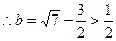 ,故矛盾.
,故矛盾.若
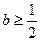 时,
时,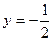 时
时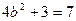 ,
, 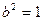
所求方程为

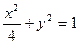
同答案

练习册系列答案
相关题目
题目内容
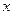 轴上,离心率
轴上,离心率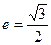 .已知点
.已知点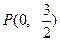 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为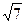 ,求这个椭圆方程.
,求这个椭圆方程.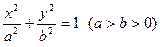 ,
, 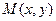 为椭圆上的点,由
为椭圆上的点,由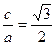 得
得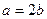
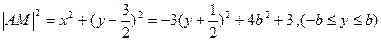
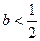 ,则当
,则当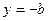 时
时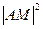 最大,即
最大,即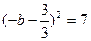 ,
, 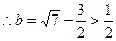 ,故矛盾.
,故矛盾.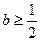 时,
时,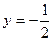 时
时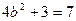 ,
,