题目内容
16. 如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形.
如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是矩形,截面A1BC是等边三角形. (I)求证:AB=AC;
(Ⅱ)若AB⊥AC,平面A1BC⊥底面ABC,求二面角B-B1C-A1的余弦值.
分析 (I)取BC中点O,连OA,OA1.证明:BC⊥平面A1OA,可得BC⊥OA,即可证明AB=AC;
(Ⅱ)分别以OA,OB,OA1为正方向建立空间直角坐标系O-xyz,求出平面BB1C的法向量、平面A1B1C的法向量,利用向量的夹角公式,即可求二面角B-B1C-A1的余弦值.
解答 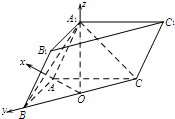 (Ⅰ)证明:取BC中点O,连OA,OA1.
(Ⅰ)证明:取BC中点O,连OA,OA1.
因为侧面BCC1B1是矩形,所以BC⊥BB1,BC⊥AA1,
因为截面A1BC是等边三角形,所以BC⊥OA1,
于是BC⊥平面A1OA,BC⊥OA,因此:AB=AC.…(4分)
(Ⅱ)解:设BC=2,则OA1=$\sqrt{3}$,由AB⊥AC,AB=AC得OA=1.
因为平面A1BC⊥底面ABC,OA1⊥BC,所以OA1⊥底面ABC.
如图,分别以OA,OB,OA1为正方向建立空间直角坐标系O-xyz. …(6分)
A(1,0,0),B(0,1,0),A1 (0,0,$\sqrt{3}$),C(0,-1,0),
$\overrightarrow{CB}$=(0,2,0),$\overrightarrow{B{B}_{1}}$=$\overrightarrow{A{A}_{1}}$=(-1,0,$\sqrt{3}$),$\overrightarrow{C{A}_{1}}$=(0,1,$\sqrt{3}$),$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{AB}$=(-1,1,0).
设平面BB1C的法向量$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{2y=0}\\{-x+\sqrt{3}z=0}\end{array}\right.$,取$\overrightarrow{m}$=($\sqrt{3}$,0,1).
同理可得平面A1B1C的法向量$\overrightarrow{n}$=(-$\sqrt{3}$,-$\sqrt{3}$,1).
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=-$\frac{\sqrt{7}}{7}$,则二面角B-B1C-A1的余弦值为-$\frac{\sqrt{7}}{7}$. …(12分)
点评 本题考查线面垂直的判定与性质,考查二面角的余弦值,考查向量法的运用,正确运用向量法是关键.

| A. | 4,0 | B. | $4\sqrt{2}$,4 | C. | $4\sqrt{2}$,0 | D. | 16,0 |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
| A. | $\frac{4}{41}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{4\sqrt{41}}{41}$ |
