题目内容
【题目】已知函数f（x）在定义域[2﹣a，3]上是偶函数，在[0，3]上单调递增，并且f（﹣m2﹣ 
）＞f（﹣m2+2m﹣2），则m的取值范围是（ ）
A.
B.
C.
D.
【答案】D
【解析】解：因为函数f（x）在定义域[2﹣a，3]上是偶函数，所以2﹣a+3=0，所以a=5．
所以 
，即f（﹣m2﹣1）＞f（﹣m2+2m﹣2），
所以函数f（x）在[﹣3，0]上单调递减，而﹣m2﹣1＜0，﹣m2+2m﹣2=﹣（m﹣1）2﹣1＜0，
所以由f（﹣m2﹣1）＞f（﹣m2+2m﹣2）得，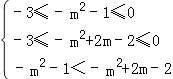
，
解得 
．
故选：D
【考点精析】关于本题考查的奇偶性与单调性的综合，需要了解奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能得出正确答案．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了50人，他们年龄的频数分布及支持“生育二胎”人数如表：
年龄 | [5，15） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
（1）由以上统计数据填下面2乘2列联表，并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异：
（2）若对年龄在[5，15），[35，45）的被调查人中各随机选取两人进行调查，记选中的4人不支持“生育二胎”人数为ξ，求随机变量ξ的分布列及数学期望；
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
参考数据：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= 
．
