题目内容
等差数列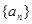 中,
中,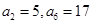 ,若数列
,若数列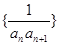 的前
的前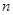 项和为
项和为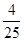 ,则
,则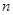 的值为
的值为
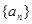 中,
中,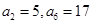 ,若数列
,若数列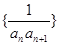 的前
的前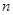 项和为
项和为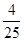 ,则
,则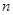 的值为
的值为| A.18 | B.16 | C.15 | D.14 |
B
根据a3=8,a7=20等差数列的通项公式为3n-1,然后根据数列的前n项的和
Sn= ,
,
因为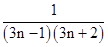 =
=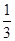 (
( )可得Sn=
)可得Sn= 解出n即可.
解出n即可.
解:设等差数列的首项为a,公差为d,
因为a2=5,a6=17,所以a+d=5,a+5d=17,解得d=3,a=2.an=3n-1;
又因为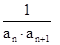 =
=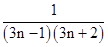 =
=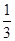 (
( ),
),
所以Sn=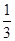 (
( )
)
=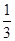 (
( -
- )=25,解得n=16
)=25,解得n=16
故选B
Sn=
 ,
,因为
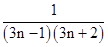 =
=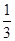 (
( )可得Sn=
)可得Sn= 解出n即可.
解出n即可.解:设等差数列的首项为a,公差为d,
因为a2=5,a6=17,所以a+d=5,a+5d=17,解得d=3,a=2.an=3n-1;
又因为
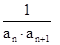 =
=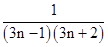 =
=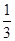 (
( ),
),所以Sn=
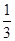 (
( )
)=
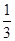 (
( -
- )=25,解得n=16
)=25,解得n=16故选B

练习册系列答案
相关题目
 满足
满足 且
且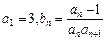 ,数列
,数列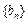 的前
的前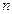 项和为
项和为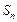 。
。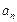 ; (2)求
; (2)求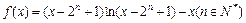 ,求证:
,求证: ≥
≥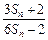 。
。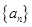 的前
的前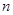 项和
项和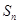
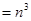 ,则
,则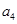 =( )
=( )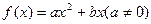 的导函数
的导函数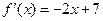 ,数列
,数列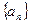 的前
的前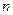 项和为
项和为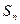 ,点
,点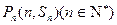 均在函数
均在函数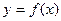 的图象上.
的图象上.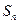 的最大值;
的最大值;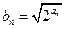 ,其中
,其中 ,求
,求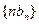 的前
的前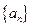 满足
满足
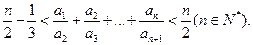
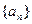 满足如图所示的程序框图.(Ⅰ)写出数列
满足如图所示的程序框图.(Ⅰ)写出数列 是等比数列,并求
是等比数列,并求 的前
的前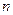 项和
项和 .
.
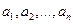 是
是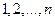 的一个排列,把排在
的一个排列,把排在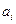
 的左边且比
的左边且比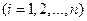 .如:在排列6,4
.如:在排列6,4 ,5,3,2,1中,5的顺序数为1 ,
,5,3,2,1中,5的顺序数为1 , 2,
2,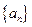 的前n项和为
的前n项和为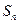 ,若
,若 ,
,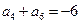 ,则当
,则当