题目内容
4.已知函数f(x)=4cosxsin(x+$\frac{π}{6}$)-1.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在x∈[$-\frac{π}{6}$,$\frac{π}{3}$]上的最值.
分析 (Ⅰ)利用三角恒等变换,化简函数f(x),求出f(x)的最小正周期;
(Ⅱ)根据x∈[-$\frac{π}{6}$,$\frac{π}{3}$],求出2x+$\frac{π}{6}$的取值范围,从而求出f(x)的取值范围,即得f(x)的最值.
解答 解:(Ⅰ)函数f(x)=4cosxsin(x+$\frac{π}{6}$)-1
=4cosx($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)-1
=$\sqrt{3}$sin2x+2cos2x-1
=$\sqrt{3}$sin2x+cos2x
=2sin(2x+$\frac{π}{6}$),
所以函数f(x)的最小正周期为
T=$\frac{2π}{2}$=π;
(Ⅱ)因为x∈[-$\frac{π}{6}$,$\frac{π}{3}$],
所以2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
所以sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
所以f(x)∈[-1,2],
即函数f(x)在x∈[-$\frac{π}{6}$,$\frac{π}{3}$]上的最大值为2,最小值为-1.
点评 本题考查了三角函数的化简与求值的应用问题,也考查了数据函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
19.函数f(x)=$\frac{x-1}{lg(x+1)}$的定义域为( )
| A. | (-1,+∞) | B. | (-1,1)∪(1,+∞) | C. | (-1,0)∪(0,+∞) | D. | (-1,0)∪(0,1)∪(1,+∞) |
9.下列四组函数中,表示同一函数的是( )
| A. | $f(x)=|x|,g(x)=\sqrt{x^2}$ | B. | f(x)=lgx2,g(x)=2lgx | ||
| C. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x-1$ | D. | $f(x)=\sqrt{x+1}•\sqrt{x-1},g(x)=\sqrt{{x^2}-1}$ |
16.如图中甲、乙、丙所示,下面是三个几何体的三视图,相应的标号是( )
①长方体 ②圆锥 ③三棱锥 ④圆柱.
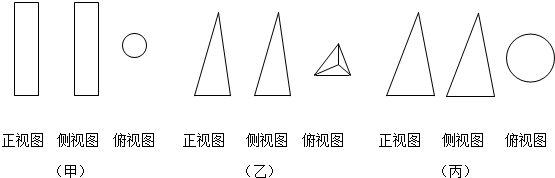
①长方体 ②圆锥 ③三棱锥 ④圆柱.

| A. | ②①③ | B. | ①②③ | C. | ③②④ | D. | ④③② |