题目内容
14．设g（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{lnx，x＞0}\end{array}\right.$，则g（g（$\frac{1}{3}$））=$\frac{1}{3}$．分析 由分段函数的性质先求出g（$\frac{1}{3}$）=ln$\frac{1}{3}$，再由对数性质求g（g（$\frac{1}{3}$））的值．
解答 解：∵g（x）=$\left\{\begin{array}{l}{{e}^{x}，x≤0}\\{lnx，x＞0}\end{array}\right.$，
∴g（$\frac{1}{3}$）=ln$\frac{1}{3}$，
g（g（$\frac{1}{3}$））=g（ln$\frac{1}{3}$）=${e}^{ln\frac{1}{3}}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质和对数性质的合理运用．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
5．已知集合A=B={（x，y）|x，y∈R}，映射f：A→B，（x，y）→（x+y，x-y），则在映射f下，象（2，1）的原象是（ ）
| A． | （$\frac{3}{2}$，-$\frac{1}{2}$） | B． | （$\frac{3}{2}$，$\frac{1}{2}$） | C． | （3，1） | D． | （1，3） |
2．函数f（x）=$sin（{2x+\frac{π}{6}}）$的最小正周期和振幅分别是（ ）
| A． | π，1 | B． | π，2 | C． | 2π，1 | D． | 2π，2 |
9．函数f（x）=$\sqrt{1-（\frac{1}{2}）^{x}}+\frac{1}{3-x}$的定义域为（ ）
| A． | （-∞，0） | B． | （0，+∞） | C． | （0，3）∪（3，+∞） | D． | [0，3）∪（3，+∞） |
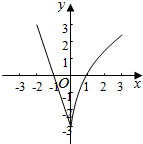函数f（x）=$\left\{\begin{array}{l}{ax+b（x≤0）}\\{lo{g}_{e}（x+\frac{1}{8}）（x＞0）}\end{array}\right.$的图象如图所示．
6．下列各点中，与点（1，2）位于直线x+y-1=0的同一侧的是（ ）
| A． | （0，0） | B． | （-1，1） | C． | （-1，3） | D． | （2，-3） |