题目内容
13.已知椭圆的一个顶点为A1(0,-$\sqrt{2}$),焦点在x轴上.若右焦点到直线x-y+2$\sqrt{2}$=0的距离3(1)求椭圆的标准方程;
(2)过点M(1,1)的直线与椭圆交于A、B两点,且M点为线段AB的中点,求直线AB的方程及|AB|的值.
分析 (1)依题意可设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}$=1,则右焦点F($\sqrt{{a}^{2}-2}$,0)由题设$\frac{|\sqrt{{a}^{2}-2}+2\sqrt{2}|}{\sqrt{2}}$=3,解出即可得出;
(2)设A(x1,y1),B(x2,y2),则x1+x2=2,y1+y2=2,$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=k,可得$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{2}$=1,$\frac{{x}_{2}^{2}}{4}+\frac{{y}_{2}^{2}}{2}$=1,相减可得k,即可得出直线AB的方程,与椭圆的方程化为:3x2-6x+1=0,利用|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$即可得出.
解答 解:(1)依题意可设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}$=1,则右焦点F($\sqrt{{a}^{2}-2}$,0)由题设$\frac{|\sqrt{{a}^{2}-2}+2\sqrt{2}|}{\sqrt{2}}$=3,解得a2=4,
故所求椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1.
(2)设A(x1,y1),B(x2,y2),则x1+x2=2,y1+y2=2,$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=k,
可得$\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{2}$=1,$\frac{{x}_{2}^{2}}{4}+\frac{{y}_{2}^{2}}{2}$=1,
相减可得:$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{2}$=0,
∴$\frac{2}{4}+\frac{2k}{2}$=0,解得k=-$\frac{1}{2}$.
∴直线AB的方程为:y-1=-$\frac{1}{2}$(x-1),化为x+2y-3=0,
联立$\left\{\begin{array}{l}{x+2y-3=0}\\{{x}^{2}+2{y}^{2}=4}\end{array}\right.$,化为:3x2-6x+1=0,
∴x1+x2=2,x1x2=-$\frac{1}{3}$
|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{(1+\frac{1}{4})[4+4×\frac{1}{3}]}$=$\frac{2\sqrt{15}}{3}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、“点差法”、中点坐标公式、斜率计算公式、弦长公式、一元二次方程的该协议书的关系,考查了推理能力与计算能力,属于中档题.

| A. | (0,1) | B. | (0,2) | C. | (2,+∞) | D. | (-∞,2) |
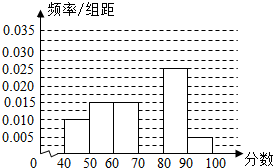 某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: