题目内容
【题目】已知椭圆E的中心在原点，焦点在x轴上，椭圆的左顶点坐标为
，离心率为
．
求椭圆E的方程；
过点
作直线l交E于P、Q两点，试问：在x轴上是否存在一个定点M，使
为定值？若存在，求出这个定点M的坐标；若不存在，请说明理由．
【答案】
1
；2
.
【解析】
设出椭圆的方程，得到关于a，c的方程组，解出即可求出椭圆方程；
假设存在符合条件的点
，设
，
，求出
，通过讨论当直线l的斜率存在时，设直线l的方程为
，联立直线和椭圆的方程，结合韦达定理求出m的值，当直线l的斜率不存在时，求出直线方程，代入检验即确定．
设椭圆E的方程为
，
由已知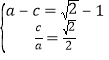得
，解得：
，
所以
．
所以椭圆E的方程为
．
假设存在符合条件的点，
设，，
则
，
，
，
当直线l的斜率存在时，设直线l的方程为，
由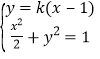
，得：
，
，
，
，
，
对于任意的k值，上式为定值，
故
，解得：
，
此时，
为定值；
当直线l的斜率不存在时，
直线l：
，
，
，
，
由，得
为定值，
综合
知，符合条件的点M存在，其坐标为
．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
