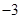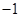题目内容
函数f(x)(x∈R)为偶函数,且f(x)在[0,+∞)上是增函数,则f(-2)、f(-π)、f(3)的大小顺序是( )
| A.f(-π)>f(3)>f(-2) | B.f(-π)>f(-2)>f(3) |
| C.f(-π)<f(3)<f(-2) | D.f(-π)<f(-2)<f(3) |
A
试题分析:函数为偶函数,则
 ,所以
,所以 ,
, 。由于f(x)在[0,+∞)上是增函数,,所以f(π)>f(3)>f(2),即f(-π)>f(3)>f(-2)。故选A。
。由于f(x)在[0,+∞)上是增函数,,所以f(π)>f(3)>f(2),即f(-π)>f(3)>f(-2)。故选A。点评:判断函数值的大小关系,主要是结合函数的单调性求解。

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
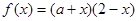 (常数
(常数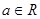 )是偶函数,则它的值域为 。
)是偶函数,则它的值域为 。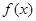 为定义在
为定义在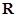 上的奇函数,当
上的奇函数,当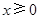 时,
时,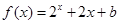 (
(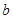 为常数),则
为常数),则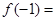
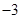
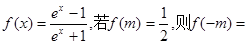 。
。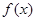 为奇函数,当
为奇函数,当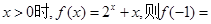 __________
__________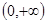 上单调递增的函数是 ( )
上单调递增的函数是 ( )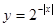
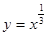
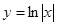
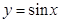
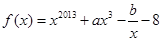 ,
,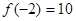 ,则
,则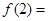 。
。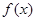 是
是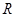 上的偶函数,且满足
上的偶函数,且满足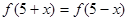 ,在[0,5]上有且只有
,在[0,5]上有且只有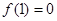 ,则
,则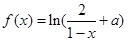 (
(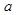 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( )