题目内容
【题目】若四位数![]() 的各位数码
的各位数码![]() 中,任三个数码皆可构成一个三角形的三条边长,则称n为“四位三角形数”.试求所有四位三角形数的个数.
中,任三个数码皆可构成一个三角形的三条边长,则称n为“四位三角形数”.试求所有四位三角形数的个数.
【答案】1681
【解析】
称(![]() )为n的数码组,则
)为n的数码组,则![]()
![]()
1.当数码组只含一个值,即![]()
![]() 时,共得9个n值.
时,共得9个n值.
2.当数码组恰含两个值![]()
i.数码组为![]() 型,则任取三个数码皆可构成三角形
型,则任取三个数码皆可构成三角形
对于每个![]() ,b可取
,b可取![]() 个值
个值
则数码组个数为![]() .
.
对于每组![]() ,b有4种占位方式.
,b有4种占位方式.
于是,这种n有![]() 个.
个.
ii.数码组为![]() 型,据构成三角形条件,有
型,据构成三角形条件,有![]() .
.
如下表,共得16个数码组,对于每组![]() ,
,![]() 有4种占位方式.
有4种占位方式.
于是,这种n有![]() 个.
个.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 |
iii.数码组为![]() 型,据构成三角形条件,有
型,据构成三角形条件,有![]() .
.
同上得16个数码组,对于每组![]() ,两个
,两个![]() 有
有![]() 种占位方式.
种占位方式.
则这种n有![]() 个.
个.
以上共计144+64+96=304个.
3.当数码组恰含三个值![]() .
.
i.数码组为![]() 型,据构成三角形条件,则有
型,据构成三角形条件,则有![]() .
.
这种![]() 有14组,每组中
有14组,每组中![]() 有
有![]() 种占位方式.
种占位方式.
于是,这种n有![]() 个.
个.
ii.数码组为![]() 型,
型,![]() .
.
此条件等价于![]() 中取3个不同的数构成三角形的方法数.
中取3个不同的数构成三角形的方法数.
有34组,每组中![]() 有
有![]() 种占位方式.
种占位方式.
于是,这种n有![]() 个.
个.
iii.数码组为![]() 型,
型,![]() ,同情况ii,有
,同情况ii,有![]() 个n值.
个n值.
以上共计168+408+408=984个.
4. ![]() 互不相同,则有
互不相同,则有![]() .
.
这种![]() 有16组,每组有
有16组,每组有![]() 种排法.
种排法.
共得![]() 个n值.
个n值.
综上,全部四位三角形数n的个数为9+304+984+384=1681(个)

【题目】为了检验两种不同的课堂教学模式对学生的成绩是否有影响,现从高二年级的甲(实行的“问题——探究式”)、乙(实行的“自学——指导式”)两个班中每班任意抽取20名学生进行测试,他们的成绩(总分150分)分布茎叶图如图所示(以十位百位为茎,个位为叶):

(1)若从参与测试的学生试卷中挑选2份卷面分数为90~100分的试着进行卷面分析,求抽取的2份试卷恰好每班1份的概率?
(2)记成绩在120分以上(包括120分)为优秀,其他的成绩为一般,请完成下面![]() 列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
列联表,并分析是否有足够的把握(90%以上)认为这两种课堂教学模式对学生的成绩有影响?
成绩 班级 | 优秀人数 | 一般人数 | 总计 |
甲班 | |||
乙班 | |||
总计 |
附: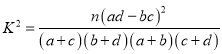
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |