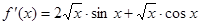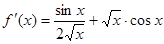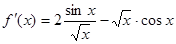题目内容
已知函数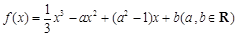
(1)若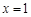 为
为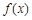 的极值点,求
的极值点,求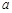 的值;
的值;
(2)若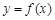 的图象在点
的图象在点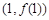 处的切线方程为
处的切线方程为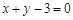 ,
,
①求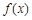 在区间
在区间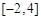 上的最大值;
上的最大值;
②求函数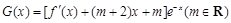 的单调区间.
的单调区间.
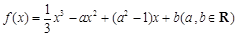
(1)若
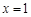 为
为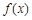 的极值点,求
的极值点,求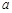 的值;
的值;(2)若
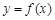 的图象在点
的图象在点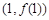 处的切线方程为
处的切线方程为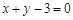 ,
,①求
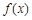 在区间
在区间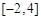 上的最大值;
上的最大值;②求函数
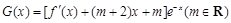 的单调区间.
的单调区间.⑴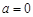 或2(2)①8②
或2(2)①8②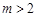 时,
时,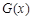 在
在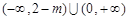 单调递减,在
单调递减,在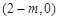 单调递增;
单调递增;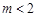 时,
时,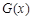 在
在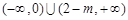 单调递减,在
单调递减,在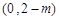 单调递增.
单调递增.
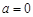 或2(2)①8②
或2(2)①8②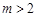 时,
时,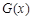 在
在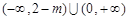 单调递减,在
单调递减,在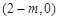 单调递增;
单调递增;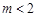 时,
时,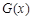 在
在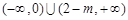 单调递减,在
单调递减,在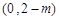 单调递增.
单调递增.⑴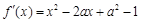 .∵
.∵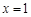 是极值点,
是极值点,
∴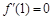 ,即
,即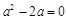 .∴
.∴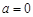 或2.
或2.
⑵∵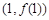 在
在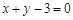 上.∴
上.∴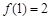
∵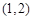 在
在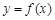 上,∴
上,∴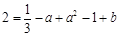
又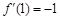 ,∴
,∴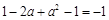
∴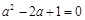 ,解得
,解得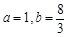
∴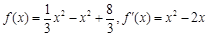
①由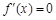 可知
可知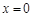 和
和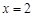 是
是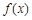 的极值点.
的极值点.
∵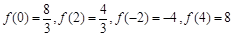
∴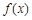 在区间
在区间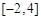 上的最大值为8.
上的最大值为8.
②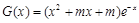
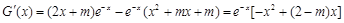
令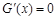 ,得
,得
当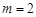 时,
时,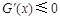 ,此时
,此时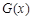 在
在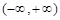 单调递减
单调递减
当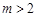 时:
时:
此时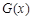 在
在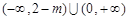 上单调递减,在
上单调递减,在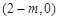 上单调递增.
上单调递增.
当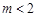 时:
时:
此时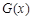 在
在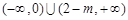 上单调递减,在
上单调递减,在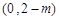 上单调递增,综上所述:当
上单调递增,综上所述:当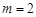 时,
时,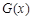 在
在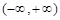 单调递减;
单调递减;
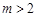 时,
时,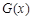 在
在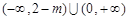 单调递减,在
单调递减,在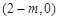 单调递增;
单调递增;
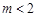 时,
时,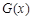 在
在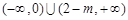 单调递减,在
单调递减,在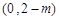 单调递增.
单调递增.
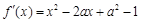 .∵
.∵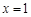 是极值点,
是极值点,∴
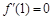 ,即
,即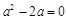 .∴
.∴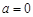 或2.
或2. ⑵∵
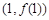 在
在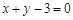 上.∴
上.∴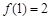
∵
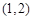 在
在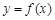 上,∴
上,∴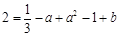
又
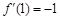 ,∴
,∴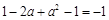
∴
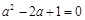 ,解得
,解得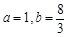
∴
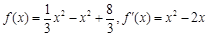
①由
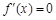 可知
可知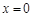 和
和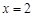 是
是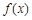 的极值点.
的极值点.∵
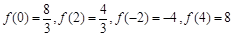
∴
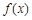 在区间
在区间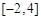 上的最大值为8.
上的最大值为8.②
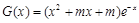
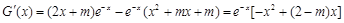
令
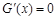 ,得
,得
当
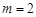 时,
时,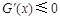 ,此时
,此时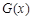 在
在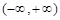 单调递减
单调递减当
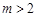 时:
时: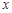 | 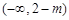 | 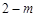 | 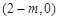 | 0 | 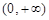 |
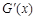 | 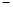 |  | + | 0 | 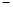 |
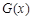 | 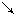 | 极小值 | 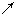 | 极大值 | 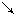 |
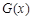 在
在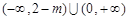 上单调递减,在
上单调递减,在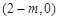 上单调递增.
上单调递增.当
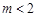 时:
时: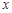 | 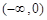 | 0 | 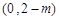 | 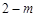 | 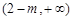 |
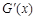 | 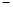 | 0 | + | 0 | 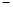 |
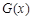 | 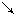 | 极小值 | 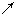 | 极大值 |  |
此时
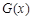 在
在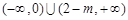 上单调递减,在
上单调递减,在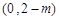 上单调递增,综上所述:当
上单调递增,综上所述:当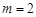 时,
时,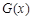 在
在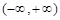 单调递减;
单调递减;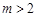 时,
时,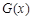 在
在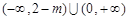 单调递减,在
单调递减,在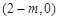 单调递增;
单调递增;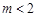 时,
时,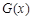 在
在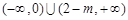 单调递减,在
单调递减,在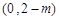 单调递增.
单调递增.
练习册系列答案
相关题目
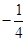 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;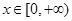 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;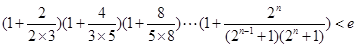 (其中
(其中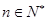 ,e是自然数对数的底数)
,e是自然数对数的底数)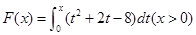 .
.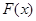 的单调区间;
的单调区间;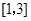 上的最值.
上的最值.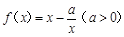 ,
,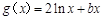 ,且直线
,且直线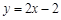 与曲线
与曲线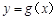 相切.
相切.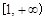 内的一切实数
内的一切实数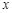 ,不等式
,不等式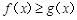 恒成立,求实数
恒成立,求实数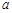 的取值范围;
的取值范围;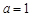 时,求最大的正整数
时,求最大的正整数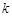 ,使得对
,使得对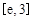 (
(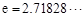 是自然对数的底数)内的任意
是自然对数的底数)内的任意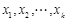 都有
都有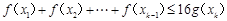 成立;
成立;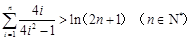 .
.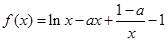 .
.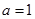 时,求曲线
时,求曲线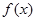 在
在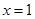 处的切线方程;
处的切线方程;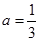 时,求函数
时,求函数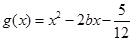 ,若对于
,若对于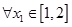 ,
,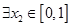 ,使
,使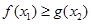 成立,求实数
成立,求实数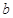 的取值范围.
的取值范围. 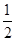 ax2+bx(a≠0),设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q,过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N,问是否存在点R,使C1在点M处的切线与C2在点N处的切线互相平行?若存在,求出点R的横坐标;若不存在,请说明理由.
ax2+bx(a≠0),设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q,过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N,问是否存在点R,使C1在点M处的切线与C2在点N处的切线互相平行?若存在,求出点R的横坐标;若不存在,请说明理由.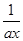 +b(a>0).
+b(a>0).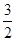 x,求a,b的值.
x,求a,b的值.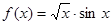 的导数为( )
的导数为( )