题目内容
已知a,b为常数,且a≠0,函数f(x)=-ax+b
+axln x,f(e)=2.
①求b;②求函数f(x)的单调区间.
+axln x,f(e)=2.
①求b;②求函数f(x)的单调区间.
①b=2②a>0时,f(x)的增区间为(1,+∞),减区间为(0,1);
a<0时,f(x)的增区间为(0,1),减区间为(1,+∞).
a<0时,f(x)的增区间为(0,1),减区间为(1,+∞).
①f(e)=2,即-ae+b+aeln e=2,∴b=2.
②由①知f(x)=-ax+axln x+2,f(x)的定义域为(0,+∞).
f′(x)=-a+a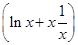 =aln x.
=aln x.
当a>0时,由f′(x)>0知x>1,由f′(x)<0知0<x<1;
当a<0时,由f′(x)>0知0<x<1,由f′(x)<0知x>1.
所以a>0时,f(x)的增区间为(1,+∞),减区间为(0,1);
a<0时,f(x)的增区间为(0,1),减区间为(1,+∞).
②由①知f(x)=-ax+axln x+2,f(x)的定义域为(0,+∞).
f′(x)=-a+a
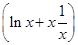 =aln x.
=aln x.当a>0时,由f′(x)>0知x>1,由f′(x)<0知0<x<1;
当a<0时,由f′(x)>0知0<x<1,由f′(x)<0知x>1.
所以a>0时,f(x)的增区间为(1,+∞),减区间为(0,1);
a<0时,f(x)的增区间为(0,1),减区间为(1,+∞).

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
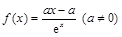
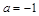 时,求函数
时,求函数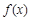 的极值;
的极值;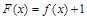 没有零点,求实数a取值范围.
没有零点,求实数a取值范围.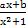 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.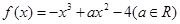 .
.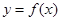 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为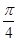 ,求
,求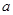 的值;
的值;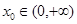 使
使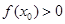 ,求
,求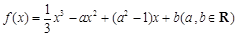
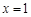 为
为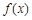 的极值点,求
的极值点,求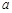 的值;
的值;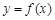 的图象在点
的图象在点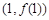 处的切线方程为
处的切线方程为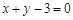 ,
,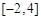 上的最大值;
上的最大值;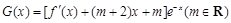 的单调区间.
的单调区间.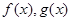 都是定义在R上的函数,
都是定义在R上的函数,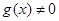 ,
,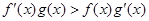 ,且
,且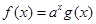
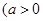 ,且
,且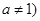 ,
,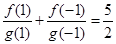 .若数列
.若数列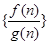 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )