题目内容
已知函数f(x)=ax2+ln(x+1).
(1)当a=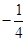 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当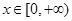 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;
(3)求证: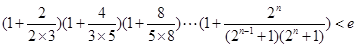 (其中
(其中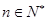 ,e是自然数对数的底数)
,e是自然数对数的底数)
(1)当a=
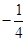 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;(2)当
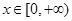 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;(3)求证:
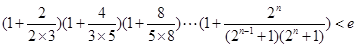 (其中
(其中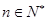 ,e是自然数对数的底数)
,e是自然数对数的底数)(1)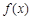 的单调递增区间为
的单调递增区间为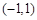 ,单调递减区间为
,单调递减区间为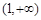 (2)
(2)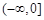 (3)见解析
(3)见解析
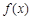 的单调递增区间为
的单调递增区间为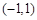 ,单调递减区间为
,单调递减区间为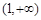 (2)
(2)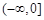 (3)见解析
(3)见解析试题分析:
(1)函数f(x)是二次与对数的结合,求单调性可以利用导数,以此先求定义域,求导,求导函数大于0与小于0分别求出单调递增与单调递减区间.
(2)要使得函数
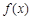 图象上的点都在
图象上的点都在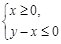 所表示的平面区域内,则当
所表示的平面区域内,则当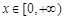 时,
时,不等式
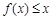 恒成立即可,即转化了恒成立问题,则只需要
恒成立即可,即转化了恒成立问题,则只需要 ,故考虑对
,故考虑对 求导求单调性来确定函数在
求导求单调性来确定函数在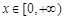 上的最大值,因为导函数含有参数a,所以在求解单调性确定最值的过程中需要讨论a的范围,讨论需从两根的大小和0的大小进行分析才能确定
上的最大值,因为导函数含有参数a,所以在求解单调性确定最值的过程中需要讨论a的范围,讨论需从两根的大小和0的大小进行分析才能确定 的最值,从而得到a的取值范围.
的最值,从而得到a的取值范围.(3)考虑把不等式两边
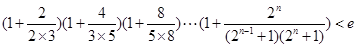 同时去对数再证明,即证明
同时去对数再证明,即证明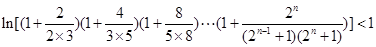 ,利用对数的乘法公式可以把不等式的左边化解成为不可求和数列的和,在利用利用(2)得到当a=0时,ln(1+x)
,利用对数的乘法公式可以把不等式的左边化解成为不可求和数列的和,在利用利用(2)得到当a=0时,ln(1+x)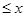 是恒成立的,把不可求和数列放缩成为可以裂项求和的数列,裂项利用
是恒成立的,把不可求和数列放缩成为可以裂项求和的数列,裂项利用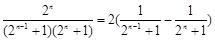 ,进而证明原不等式.
,进而证明原不等式.试题解析:
(1)当
 时,
时,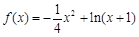 (
(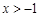 ),
),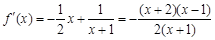 (
(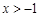 ), 1分
), 1分由
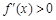 解得
解得 ,由
,由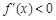 解得
解得 .
.故函数
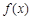 的单调递增区间为
的单调递增区间为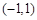 ,单调递减区间为
,单调递减区间为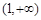 . 3分
. 3分(2)因函数
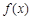 图象上的点都在
图象上的点都在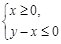 所表示的平面区域内,则当
所表示的平面区域内,则当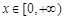 时,
时,不等式
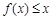 恒成立,即
恒成立,即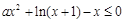 恒成立,
恒成立,设
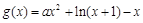 (
(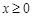 ),只需
),只需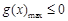 即可. 4分
即可. 4分由
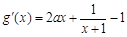
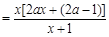 ,
,(ⅰ)当
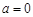 时,
时,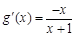 ,当
,当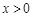 时,
时,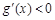 ,
,函数
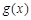 在
在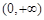 上单调递减,故
上单调递减,故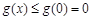 成立. 5分
成立. 5分(ⅱ)当
 时,由
时,由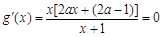 ,因
,因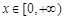 ,所以
,所以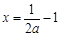 ,
,①
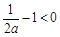 ,即
,即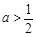 时,在区间
时,在区间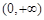 上,
上,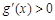 ,则函数
,则函数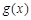 在
在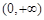 上单调递增,
上单调递增,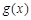 在
在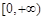 上无最大值(或:当
上无最大值(或:当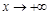 时,
时,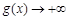 ),此时不满足条件;
),此时不满足条件;②若
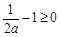 ,即
,即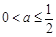 时,函数
时,函数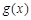 在
在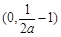 上单调递减,
上单调递减,在区间
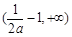 上单调递增,同样
上单调递增,同样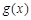 在
在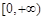 上无最大值,不满足条件. 8分
上无最大值,不满足条件. 8分(ⅲ)当
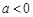 时,由
时,由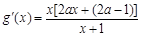 ,∵
,∵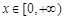 ,∴
,∴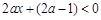 ,
,∴
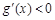 ,故函数
,故函数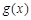 在
在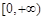 上单调递减,故
上单调递减,故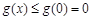 成立.
成立.综上所述,实数
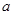 的取值范围是
的取值范围是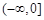 . 10分
. 10分(3)据(2)知当
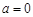 时,
时,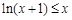 在
在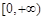 上恒成立.
上恒成立.(或另证
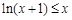 在区间
在区间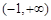 上恒成立), 11分
上恒成立), 11分又
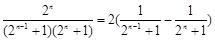 ,
,∵
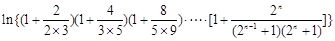
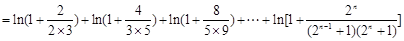
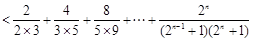
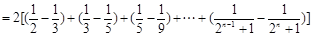
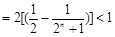 ,
,
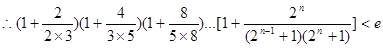 . 14分
. 14分
练习册系列答案
相关题目
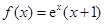 .
.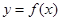 在点
在点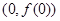 处的切线方程;
处的切线方程;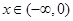 ,都有
,都有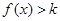 ,求
,求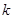 的取值范围.
的取值范围.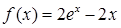 ,
,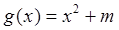 (
(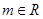 ).
).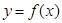 的单调性;
的单调性;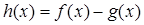 ,
,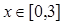 ,当函数
,当函数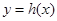 有零点时,求实数
有零点时,求实数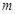 的最大值.
的最大值.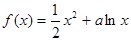 ,
,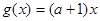 .
.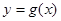 恰好为曲线
恰好为曲线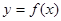 的切线时,求实数
的切线时,求实数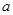 的值;
的值;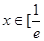 ,
,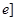 时(其中无理数
时(其中无理数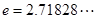 ),
),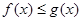 恒成立,试确定实数
恒成立,试确定实数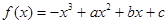 在
在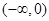 上是减函数,在
上是减函数,在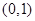 上是增函数,函数
上是增函数,函数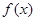 在
在 上有三个零点,且
上有三个零点,且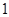 是其中一个零点.
是其中一个零点.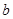 的值;
的值;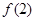 的取值范围;
的取值范围;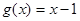 ,且
,且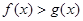 的解集为
的解集为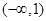 ,求实数
,求实数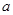 的取值范围.
的取值范围.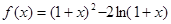
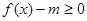 在
在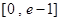 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;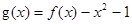 ,若关于x的方程
,若关于x的方程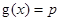 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.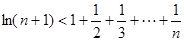
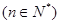
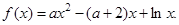
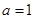 时,求曲线
时,求曲线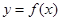 在点
在点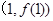 处的切线方程;
处的切线方程;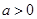 时,若
时,若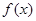 在区间
在区间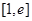 上的最小值为-2,求
上的最小值为-2,求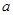 的取值范围;
的取值范围; 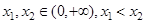 ,且
,且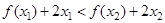 恒成立,求
恒成立,求
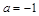 时,求函数
时,求函数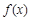 的极值;
的极值;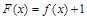 没有零点,求实数a取值范围.
没有零点,求实数a取值范围.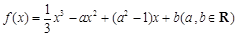
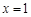 为
为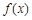 的极值点,求
的极值点,求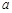 的值;
的值;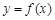 的图象在点
的图象在点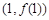 处的切线方程为
处的切线方程为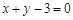 ,
,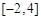 上的最大值;
上的最大值; 的单调区间.
的单调区间.